Question

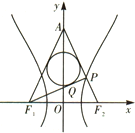如图，已知双曲线

x2

a2

-

y2

b2

=1（a＞0，b＞0）的左右焦点分别为F₁，F₂，|F₁F₂|=4，P是双曲线右支上一点，直线PF₂交y轴于点A，△AF₁P的内切圆切边PF₁于点Q，若|PQ|=1，则双曲线的渐近线方程为（　　）

• A、y=±

  3

  3

  x
• B、y=±3x
• C、y=±

  1

  3

  x
• D、y=±

  3

  x

Answer 1

考点：双曲线的简单性质

专题：直线与圆,圆锥曲线的定义、性质与方程

分析：设内切圆与AP切于点M，与AF₁切于点N，|PF₁|=m，|QF₁|=n，由双曲线的定义可得|PF₁|-|PF₂|=2a，即有m-（n-1）=2a，①运用对称性和切线的性质可得m-1=n，②，可得a=1，再由c=2，可得b，结合渐近线方程即可得到．

解答： 解：设内切圆与AP切于点M，与AF₁切于点N，
|PF₁|=m，|QF₁|=n，
由双曲线的定义可得|PF₁|-|PF₂|=2a，即有m-（n-1）=2a，①
由切线的性质可得|AM|=|AN|，|NF₁|=|QF₁|=n，|MP|=|PQ|=1，
|MF₂|=|NF₁|=n，
即有m-1=n，②
由①②解得a=1，
由|F₁F₂|=4，则c=2，
b=

c2-a2

=

3

，
由双曲线

x2

a2

-

y2

b2

=1的渐近线方程为y=±

b

a

x，
即有渐近线方程为y=±

3

x．
故选D．

点评：本题考查双曲线的方程和性质，考查切线的性质，运用对称性和双曲线的定义是解题的关键．