题目内容
已知sinα=
,α∈(
,π)
(1)求tanα及tan2α;
(2)求
的值.
2
| ||
| 5 |
| π |
| 2 |
(1)求tanα及tan2α;
(2)求
2cos(
| ||
sin(
|
考点:同角三角函数基本关系的运用,运用诱导公式化简求值
专题:三角函数的求值
分析:(1)由sinα的值及α的范围,利用同角三角函数间的基本关系求出cosα的值,进而求出tanα的值,再利用二倍角的正切函数公式求出tan2α的值即可;
(2)原式利用诱导公式化简,再利用同角三角函数间的基本关系变形,把tanα的值代入计算即可求出值.
(2)原式利用诱导公式化简,再利用同角三角函数间的基本关系变形,把tanα的值代入计算即可求出值.
解答:
解:(1)∵sin2α+cos2α=1,sinα=
,
∴cos2α=1-sin2α=
,
又α∈(
,π),
∴cosα=-
,
∴tanα=
=-2,
则tan2α=
=
=
;
(2)∵tanα=-2,
∴原式=
=
=
=
.
2
| ||
| 5 |
∴cos2α=1-sin2α=
| 1 |
| 5 |
又α∈(
| π |
| 2 |
∴cosα=-
| ||
| 5 |
∴tanα=
| sinα |
| cosα |
则tan2α=
| 2tanα |
| 1-tan2α |
| -4 |
| 1-4 |
| 4 |
| 3 |
(2)∵tanα=-2,
∴原式=
| -2sinα-cosα |
| cosα-3sinα |
| -2tanα-1 |
| 1-3tanα |
| 4-1 |
| 1+6 |
| 3 |
| 7 |
点评:此题考查了同角三角函数基本关系的运用,以及运用诱导公式化简求值,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
设f(x)=
,则f(f(2))=( )
|
| A、-1 | B、-2 | C、1 | D、2 |
已知不等式
>0的解集为(-1,2),则二项式(ax-
)6展开式的常数项是( )
| x-2 |
| ax-1 |
| 1 |
| x2 |
| A、5 | B、-5 | C、15 | D、25 |
已知p:函数f(x)=|x+a|在(-∞,-1)上是单调函数;q:函数g(x)=loga(x+1)(a>0且a≠1)在(-1,+∞)上是增函数,则¬p成立是q成立的( )
| A、充分不必要 |
| B、必要不充分 |
| C、充要条件 |
| D、既不充分也不必要 |
下列函数中,为奇函数的是( )
| A、f(x)=x2-2x | ||
B、f(x)=
| ||
C、f(x)=x-
| ||
| D、f(x)=x2+2 |
已知函数f(x)=
sinxcosx+
cos2x,若将其图象向右平移φ(φ>0)个单位所得的图象关于原点对称,则φ的最小值为( )
| 3 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
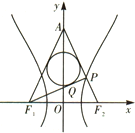 如图,已知双曲线
如图,已知双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、y=±
| ||||
| B、y=±3x | ||||
C、y=±
| ||||
D、y=±
|