题目内容
在直角坐标系xOy中,l是过定点P(4,2)且倾斜角为α的直线;在极坐标系(以坐标原点O为极点,以x轴非负半轴为极轴,取相同单位长度)中,曲线C的极坐标方程为ρ=4cosθ
(Ⅰ)写出直线l的参数方程,并将曲线C的方程化为直角坐标方程;
(Ⅱ)若曲线C与直线相交于不同的两点M、N,求|PM|+|PN|的取值范围.
(Ⅰ)写出直线l的参数方程,并将曲线C的方程化为直角坐标方程;
(Ⅱ)若曲线C与直线相交于不同的两点M、N,求|PM|+|PN|的取值范围.
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:(I)直线l的参数方程为
(t为参数).曲线C的极坐标方程ρ=4cosθ可化为ρ2=4ρcosθ.把x=ρcosθ,y=ρsinθ代入曲线C的极坐标方程即可得出.
(II)把直线l的参数方程为
(t为参数)代入圆的方程可得:t2+4(sinα+cosα)t+4=0.由于曲线C与直线相交于不同的两点M、N,可得△=16(sinα+cosα)2-16>0,可得α∈(0,
).
利用根与系数的关系t1+t2=-4(sinα+cosα),t1t2=4.及|PM|+|PN|=|t1|+|t2|=|t1+t2|=4|sinα+cosα|=4
sin(α+
),即可得出.
|
(II)把直线l的参数方程为
|
| π |
| 2 |
利用根与系数的关系t1+t2=-4(sinα+cosα),t1t2=4.及|PM|+|PN|=|t1|+|t2|=|t1+t2|=4|sinα+cosα|=4
| 2 |
| π |
| 4 |
解答:
解:(I)直线l的参数方程为
(t为参数).
曲线C的极坐标方程ρ=4cosθ可化为ρ2=4ρcosθ.
把x=ρcosθ,y=ρsinθ代入曲线C的极坐标方程可得x2+y2=4x,即(x-2)2+y2=4.
(II)把直线l的参数方程为
(t为参数)代入圆的方程可得:t2+4(sinα+cosα)t+4=0.
∵曲线C与直线相交于不同的两点M、N,
∴△=16(sinα+cosα)2-16>0,
∴sinαcosα>0,又α∈[0,π),
∴α∈(0,
).
又t1+t2=-4(sinα+cosα),t1t2=4.
∴|PM|+|PN|=|t1|+|t2|=|t1+t2|=4|sinα+cosα|=4
sin(α+
),
∵α∈(0,
),∴(α+
)∈(
,
),
∴sin(α+
)∈(
,1].
∴|PM|+|PN|的取值范围是(4,4
].
|
曲线C的极坐标方程ρ=4cosθ可化为ρ2=4ρcosθ.
把x=ρcosθ,y=ρsinθ代入曲线C的极坐标方程可得x2+y2=4x,即(x-2)2+y2=4.
(II)把直线l的参数方程为
|
∵曲线C与直线相交于不同的两点M、N,
∴△=16(sinα+cosα)2-16>0,
∴sinαcosα>0,又α∈[0,π),
∴α∈(0,
| π |
| 2 |
又t1+t2=-4(sinα+cosα),t1t2=4.
∴|PM|+|PN|=|t1|+|t2|=|t1+t2|=4|sinα+cosα|=4
| 2 |
| π |
| 4 |
∵α∈(0,
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴sin(α+
| π |
| 4 |
| ||
| 2 |
∴|PM|+|PN|的取值范围是(4,4
| 2 |
点评:本题考查了直线的参数方程、圆的极坐标方程、直线与圆相交弦长问题,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=2x2-kx-8在区间[1,2]上不单调,则实数k的取值范围为( )
| A、[4,8] |
| B、(-∞,4]∪[8,+∞) |
| C、(-∞,4)∪(8,+∞) |
| D、(4,8) |
一个三棱柱的侧棱垂直于底面,且所有棱长都为a,则此三棱柱的外接球的表面积为( )
| A、πa2 | ||
| B、15πa2 | ||
C、
| ||
D、
|
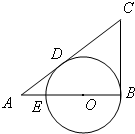 如图,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,AD=2,AE=1,则AB的长为
如图,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,AD=2,AE=1,则AB的长为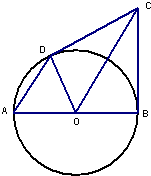 (几何证明选讲选做题)如图,AB是圆O的直径,BC是圆O的切线,切点为B,OC平行于弦AD,若OB=3,OC=5,则CD=
(几何证明选讲选做题)如图,AB是圆O的直径,BC是圆O的切线,切点为B,OC平行于弦AD,若OB=3,OC=5,则CD=