题目内容
函数f(x)=
( )
| 2x-2-x |
| 3 |
| A、是奇函数,在(-∞,+∞)上是增函数 |
| B、是偶函数,在(-∞,+∞)上是减函数 |
| C、是偶函数,在(-∞,+∞)上是增函数 |
| D、是奇函数,在(-∞,+∞)上是减函数 |
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:函数的性质及应用
分析:现根据f(-x)=-f(x),可得函数为奇函数;再根据
•2x在R上是增函数,y=
•2-x在R上是减函数,可得f(x)的单调性.
| 1 |
| 3 |
| 1 |
| 3 |
解答:
解:由函数的解析式可得 f(-x)=
=-
=-f(x),
故函数f(x)为奇函数.
再根据y=
•2x在R上是增函数,y=
•2-x在R上是减函数,
故函数f(x)=
=
•2x-
•2-x 在R上是增函数,
故选:A.
| 2-x-2x |
| 3 |
| 2x-2-x |
| 3 |
故函数f(x)为奇函数.
再根据y=
| 1 |
| 3 |
| 1 |
| 3 |
故函数f(x)=
| 2x-2-x |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
故选:A.
点评:本题主要考查函数的奇偶性的定义和判断,函数的单调性的判断,属于中档题.

练习册系列答案
相关题目
过点M(x,0)向圆x2+y2-12y+27=0作两条切线,则两切线的最大夹角为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R),则圆C与直线l的位置关系( )
| A、相离 | B、相切 |
| C、相交 | D、无法判断 |
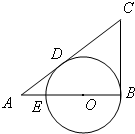 如图,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,AD=2,AE=1,则AB的长为
如图,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,AD=2,AE=1,则AB的长为