题目内容
设Sn等比数列{an}的前n项和,且a2=
,S2=
(1)求数列{an}的通项;
(2)设bn=
,求数列{bn}的前n项和Sn.
| 1 |
| 9 |
| 4 |
| 9 |
(1)求数列{an}的通项;
(2)设bn=
| n |
| an |
考点:数列的求和
专题:计算题,等差数列与等比数列
分析:(1)设首项为a1,公比为q,由a2=
,S2=
可求得
,于是可求数列{an}的通项;
(2)由bn=
=
=n•3n,知Sn=3+2×32+3×33+…+n•3n,利用错位相减法即可求得数列{bn}的前n项和Sn.
| 1 |
| 9 |
| 4 |
| 9 |
|
(2)由bn=
| n |
| an |
| n | ||
|
解答:
解:(1)设首项为a1,公比为q,由a2=
,S2=
,
得:
,
解得:
,
∴an=
;.
(2)∵bn=
=
=n•3n,
∴Sn=3+2×32+3×33+…+n•3n,①
∴3Sn=32+2×33+3×34+…+(n-1)•3n+n•3n+1,②
②-①得2Sn=n•3n+1-(3+32+33+…+3n)=n•3n+1-
=
+
,
∴Sn=
+
.
| 1 |
| 9 |
| 4 |
| 9 |
得:
|
解得:
|
∴an=
| 1 |
| 3n |
(2)∵bn=
| n |
| an |
| n | ||
|
∴Sn=3+2×32+3×33+…+n•3n,①
∴3Sn=32+2×33+3×34+…+(n-1)•3n+n•3n+1,②
②-①得2Sn=n•3n+1-(3+32+33+…+3n)=n•3n+1-
| 3(1-3n) |
| 1-3 |
| (2n-1)×3n+1 |
| 2 |
| 3 |
| 2 |
∴Sn=
| (2n-1)×3n+1 |
| 4 |
| 3 |
| 4 |
点评:本题考查数列的求和,着重考查等比数列的通项公式与错位相减法求和,考查方程思想与运算能力,属于中档题.

练习册系列答案
相关题目
已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R),则圆C与直线l的位置关系( )
| A、相离 | B、相切 |
| C、相交 | D、无法判断 |
 某个实心零部件的形状是如图所示的几何体,其下部是底面均是正方形,侧面是全等的等腰梯形的四棱台A1B1C1D1-ABCD,上面是一个底面与四棱台的上底面重合,侧面是全等的矩形的四棱柱ABCD-A2B2C2D2.现需要对该零部件表面进行防腐处理,已知AB=10,A1B1=20,AA2=30,AA1=13(单位:厘米),每平方厘米的加工处理费为0.20元,需加工处理费多少元?
某个实心零部件的形状是如图所示的几何体,其下部是底面均是正方形,侧面是全等的等腰梯形的四棱台A1B1C1D1-ABCD,上面是一个底面与四棱台的上底面重合,侧面是全等的矩形的四棱柱ABCD-A2B2C2D2.现需要对该零部件表面进行防腐处理,已知AB=10,A1B1=20,AA2=30,AA1=13(单位:厘米),每平方厘米的加工处理费为0.20元,需加工处理费多少元?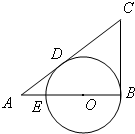 如图,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,AD=2,AE=1,则AB的长为
如图,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,AD=2,AE=1,则AB的长为