题目内容
在极坐标系中,以(
,
)为圆心,
为半径的圆的方程为 .
| a |
| 2 |
| π |
| 2 |
| a |
| 2 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:如图所示,由于∠APO是⊙O的直径AO所对的圆周角,可得∠APO=
.可得ρ=acos(
-θ).
| π |
| 2 |
| π |
| 2 |
解答:
解:如图所示,
∵∠APO是⊙O的直径AO所对的圆周角,
∴∠APO=
.
∴ρ=acos(
-θ)=asinθ.
∴ρ=asinθ.
故答案为:ρ=asinθ.

∵∠APO是⊙O的直径AO所对的圆周角,
∴∠APO=
| π |
| 2 |
∴ρ=acos(
| π |
| 2 |
∴ρ=asinθ.
故答案为:ρ=asinθ.
点评:本题考查了圆的极坐标方程,属于基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
一个三棱柱的侧棱垂直于底面,且所有棱长都为a,则此三棱柱的外接球的表面积为( )
| A、πa2 | ||
| B、15πa2 | ||
C、
| ||
D、
|
将直线2x-y+λ=0沿x轴向左平移一个单位,所得直线与曲线C:
(θ为参数)相切,则实数λ的值为( )
|
| A、-7或3 | B、-2或8 |
| C、0或10 | D、1或11 |
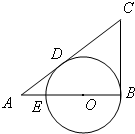 如图,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,AD=2,AE=1,则AB的长为
如图,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,AD=2,AE=1,则AB的长为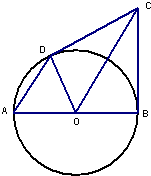 (几何证明选讲选做题)如图,AB是圆O的直径,BC是圆O的切线,切点为B,OC平行于弦AD,若OB=3,OC=5,则CD=
(几何证明选讲选做题)如图,AB是圆O的直径,BC是圆O的切线,切点为B,OC平行于弦AD,若OB=3,OC=5,则CD=