题目内容
下列说法中正确的是( )
| A、若p∨q为真命题,则p,q均为真命题 |
| B、命题“?x0∈R,2x0≤0”的否定是“?x∈R,2x>0” |
| C、“a≥5”是“?x∈[1,2],x2-a≤0恒成立“的充要条件 |
| D、在△ABC中,“a>b”是“sinA>sinB”的必要不充分条件 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:A.若p∨q为真命题,则p或q为真命题,即可判断出;
B.利用特称命题的否定是全称命题即可得出;
C.“a≥5”是“?x∈[1,2],x2-a≤0恒成立“的充分不必要条件;
D.在△ABC中,“a>b”?A>B.利用角的范围及其正弦余弦函数的单调性和和差化积即可得出.
B.利用特称命题的否定是全称命题即可得出;
C.“a≥5”是“?x∈[1,2],x2-a≤0恒成立“的充分不必要条件;
D.在△ABC中,“a>b”?A>B.利用角的范围及其正弦余弦函数的单调性和和差化积即可得出.
解答:
解:A.若p∨q为真命题,则p或q为真命题,因此不正确;
B.命题“?x0∈R,2x0≤0”的否定是“?x∈R,2x>0”,正确;
C.“a≥5”是“?x∈[1,2],x2-a≤0恒成立“的充分不必要条件,因此不正确;
D.在△ABC中,“a>b”?A>B.
∴0<
<
,0<
<
,
∴cos
>0,sin
>0,
∴sinA-sinB=2cos
sin
>0.
因此“a>b”是“sinA>sinB”的充要条件,因此D不正确.
综上可知:只有B正确.
故选:B.
B.命题“?x0∈R,2x0≤0”的否定是“?x∈R,2x>0”,正确;
C.“a≥5”是“?x∈[1,2],x2-a≤0恒成立“的充分不必要条件,因此不正确;
D.在△ABC中,“a>b”?A>B.
∴0<
| A+B |
| 2 |
| π |
| 2 |
| A-B |
| 2 |
| π |
| 2 |
∴cos
| A+B |
| 2 |
| A-B |
| 2 |
∴sinA-sinB=2cos
| A+B |
| 2 |
| A-B |
| 2 |
因此“a>b”是“sinA>sinB”的充要条件,因此D不正确.
综上可知:只有B正确.
故选:B.
点评:本题考查了简易逻辑有关知识、三角函数的单调性及其和差化积,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列几何体的主视图与众不同的是( )
A、 |
B、 |
C、 |
D、 |
关于直线a,b及平面α,β,下列命题中正确的是( )
| A、若a∥α,α∩β=b,则a∥b |
| B、若a∥α,b∥α,则a∥b |
| C、若a⊥α,a∥β,则α⊥β |
| D、若a∥α,b⊥a,则b⊥α |
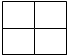 由单位正方体(棱长为1的正方体)叠成的积木堆的正视图与侧视图均为图所示,则该积木堆中单位正方体的最少个数为( )
由单位正方体(棱长为1的正方体)叠成的积木堆的正视图与侧视图均为图所示,则该积木堆中单位正方体的最少个数为( )| A、5个 | B、4个 | C、6个 | D、7个 |
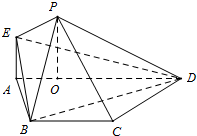 如图,在等腰梯形ABCD中,AD∥BC,AB=BC=CD=
如图,在等腰梯形ABCD中,AD∥BC,AB=BC=CD=