题目内容
8．若角θ满足$\frac{2cos（\frac{π}{2}-θ）+cosθ}{2sin（π+θ）-3cos（π-θ）}$=3，则tanθ的值为（ ）| A． | -$\frac{5}{4}$ | B． | -2 | C． | -$\frac{1}{2}$ | D． | 1 |
分析 利用诱导公式化简已知三角等式，化弦为切求得答案．
解答 解：由$\frac{2cos（\frac{π}{2}-θ）+cosθ}{2sin（π+θ）-3cos（π-θ）}$=3，得$\frac{2sinθ+cosθ}{-2sinθ+3cosθ}=3$，
分子分母同时除以cosθ，得$\frac{2tanθ+1}{-2tanθ+3}=3$，
解得：tanθ=1．
故选：D．
点评 本题考查三角函数的化简与求值，熟记三角函数的诱导公式是关键，是基础题．
练习册系列答案
相关题目
3．若集合A={1，a，b}，B={1，-1，2}，且B=A，则a+b的值为（ ）
| A． | 3 | B． | 1 | C． | 0 | D． | 不能确定 |
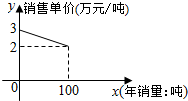某种产品的成本f1（x）（万元）与年产量x（吨）之间的函数关系是f1（x）=$\frac{1}{100}$x2，该产品的销售单价f2（x）可以表示为关于年销量的一次函数，其部分图象如图所示，且生产的产品都能在当年销售完．
17．命题“?x0∈R，x${\;}_{0}^{2}$+2x0≥2”的否定为（ ）
| A． | ?x0∈R，${x}_{0}^{2}$+2x0≤2 | B． | ?x∈R，x2+2x≥2 | ||
| C． | ?x0∈R，${x}_{0}^{2}$+2x0＜2 | D． | ?x∈R，x2+2x＜2 |