题目内容
20．
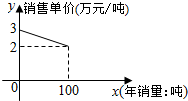某种产品的成本f1（x）（万元）与年产量x（吨）之间的函数关系是f1（x）=$\frac{1}{100}$x2，该产品的销售单价f2（x）可以表示为关于年销量的一次函数，其部分图象如图所示，且生产的产品都能在当年销售完．（1）求f2（x）的解析式及定义域；
（2）当年产量为多少吨时，所获利润s（万元）最大（注：利润=收入-成本）；并求出s的最大值．
分析 （1）由题意可设：f2（x）=kx+b（k≠0），由于图象经过点（0，3），（100，2）．代入解出即可得出．令f2（x）＞0，解得函数的定义域．
（2）设年产量为x吨，s=x•f2（x）-f1（x）=-$\frac{1}{50}$（x-75）2+$\frac{225}{2}$，利用二次函数的单调性即可得出．
解答 解：（1）由题意可设：f2（x）=kx+b（k≠0），由于图象经过点（0，3），（100，2）．
∴$\left\{\begin{array}{l}{3=b}\\{2=100k+b}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=-\frac{1}{100}}\\{b=3}\end{array}\right.$，
∴f2（x）=$-\frac{1}{100}x$+3，令f2（x）=$-\frac{1}{100}x$+3＞0，解得0＜x＜300，其定义域为（0，300）．
（2）设年产量为x吨，s=x•f2（x）-f1（x）=$x（-\frac{1}{100}x+3）$-$\frac{1}{100}$x2=$-\frac{1}{50}{x}^{2}$+3x=-$\frac{1}{50}$（x-75）2+$\frac{225}{2}$，
∴当x=75时，s取得最大值$\frac{225}{2}$（万元）．
点评 本题考查了一次函数与二次函数的图象与性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
8．若函数y=x2+2（a-b）x+a2与x轴有两个交点，且b＞0，则a与b的关系是（ ）
| A． | a＞b | B． | a$＜\frac{b}{2}$ | C． | a$＞\frac{b}{2}$ | D． | a＜b |
8．若角θ满足$\frac{2cos（\frac{π}{2}-θ）+cosθ}{2sin（π+θ）-3cos（π-θ）}$=3，则tanθ的值为（ ）
| A． | -$\frac{5}{4}$ | B． | -2 | C． | -$\frac{1}{2}$ | D． | 1 |
5．要完成下列3项抽样调查：
①从某班10名班干部中随机抽取3人进行一项问卷调查．
②科技报告厅的座位有60排，每排有50个，某次报告会恰好坐满听众，报告会结束后，为了解听众意见，需要随机抽取30名听众进行座谈．
③某高中共有160名教职工，其中教师120名，行政人员16名，后勤人员24名．为了解教职工的文化水平，拟随机抽取一个容量为40的样本．
较为合理的抽样方法是（ ）
①从某班10名班干部中随机抽取3人进行一项问卷调查．
②科技报告厅的座位有60排，每排有50个，某次报告会恰好坐满听众，报告会结束后，为了解听众意见，需要随机抽取30名听众进行座谈．
③某高中共有160名教职工，其中教师120名，行政人员16名，后勤人员24名．为了解教职工的文化水平，拟随机抽取一个容量为40的样本．
较为合理的抽样方法是（ ）
| A． | ①简单随机抽样，②分层抽样，③系统抽样 | |
| B． | ①简单随机抽样，②系统抽样，③分层抽样 | |
| C． | ①系统抽样，②简单随机抽样，③分层抽样 | |
| D． | ①分层抽样，②系统抽样，③简单随机抽样 |