题目内容
20.已知数列{an}的通项公式为an=$\frac{48}{(n+2)^{2}-4}$,Sn是数列{an}的前n项的和,则与S98最接近的整数是( )| A. | 20 | B. | 21 | C. | 24 | D. | 25 |
分析 由题意可得,an=$\frac{48}{(n+2)^{2}-4}$=12($\frac{1}{n}$-$\frac{1}{n+4}$),利用裂项求和可得Sn=25-12($\frac{1}{n+1}$+$\frac{1}{n+2}$+$\frac{1}{n+3}$+$\frac{1}{n+4}$),求出结果再跟选项相比较即可.
解答 解:∵an=$\frac{48}{(n+2)^{2}-4}$=12($\frac{1}{n}$-$\frac{1}{n+4}$)
∴Sn=12(1-$\frac{1}{5}$+$\frac{1}{2}$-$\frac{1}{6}$+$\frac{1}{3}$-$\frac{1}{7}$+$\frac{1}{4}$-$\frac{1}{8}$+…+$\frac{1}{n}$-$\frac{1}{n+4}$)=12(1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$-$\frac{1}{n+3}$-$\frac{1}{n+4}$)=25-12($\frac{1}{n+1}$+$\frac{1}{n+2}$+$\frac{1}{n+3}$+$\frac{1}{n+4}$)
∴与S98最接近的整数是25;
故选D.
点评 本题主要考查了数列的求和,而求和方法的选择最关键的是观察通项公式,正确裂项.

练习册系列答案
相关题目
1.已知变量x,y满足线性约束条件$\left\{\begin{array}{l}{y≥a(x-3)}\\{x+y≤3}\\{x≥1}\end{array}\right.$其中a>0,当z=2x+y的最小值为1时,a等于( )
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
2.等比数列{an}的前n项和为Sn,若a2=3,S3=13,则log3a3的值为( )
| A. | 0 | B. | 2 | C. | 0或2 | D. | 1或2 |
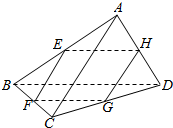 如图所示,在三棱锥A-BCD中,E,F,G,H分别是棱AB,BC,CD,DA的中点,则当AC,BD满足条件AC=BD时,四边形EFGH为菱形.
如图所示,在三棱锥A-BCD中,E,F,G,H分别是棱AB,BC,CD,DA的中点,则当AC,BD满足条件AC=BD时,四边形EFGH为菱形.