题目内容
已知椭圆
+
=1(a>b>0)离心率为
,短轴长为2,直线l:y=x+m,
(1)求椭圆的标准方程;
(2)当直线l与椭圆有公共点时,求实数m的取值范围;
(3)若直线l过椭圆右焦点,并与椭圆交于A、B两点,求弦AB之长.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
(1)求椭圆的标准方程;
(2)当直线l与椭圆有公共点时,求实数m的取值范围;
(3)若直线l过椭圆右焦点,并与椭圆交于A、B两点,求弦AB之长.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知得
,由此能求出椭圆的标准方程.
(2)联立
,得7x2+8mx+4m2-4=0,由直线l与椭圆有公共点,得△=64m2-28(4m2-4)≥0,由此能求出实数m的取值范围.
(3)联立
,得7x2-
x-
=0,由此能求出|AB|.
|
(2)联立
|
(3)联立
|
8
| ||
| 3 |
| 8 |
| 3 |
解答:
解:(1)∵椭圆
+
=1(a>b>0)离心率为
,短轴长为2,
∴
,解得a2=
,b2=1,
∴椭圆的标准方程为
+y2=1.
(2)联立
,得7x2+8mx+4m2-4=0,
∵直线l与椭圆有公共点,
∴△=64m2-28(4m2-4)≥0,
解得-
<m<
.
∴实数m的取值范围是(-
,
).
(3)∵直线l:y=x+m过椭圆右焦点F2(
,0),
∴m=-
,y=x-
,
联立
,得7x2-
x-
=0,
设A(x1,y1),B(x2,y2),则x1+x2=
,x1x2=-
,
∴|AB|=
=
.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
∴
|
| 4 |
| 3 |
∴椭圆的标准方程为
| x2 | ||
|
(2)联立
|
∵直线l与椭圆有公共点,
∴△=64m2-28(4m2-4)≥0,
解得-
| ||
| 3 |
| ||
| 3 |
∴实数m的取值范围是(-
| ||
| 3 |
| ||
| 3 |
(3)∵直线l:y=x+m过椭圆右焦点F2(
| ||
| 3 |
∴m=-
| ||
| 3 |
| ||
| 3 |
联立
|
8
| ||
| 3 |
| 8 |
| 3 |
设A(x1,y1),B(x2,y2),则x1+x2=
8
| ||
| 21 |
| 8 |
| 21 |
∴|AB|=
(1+1)[(
|
8
| ||
| 7 |
点评:本题考查椭圆方程的求法,考查实数的取值范围的求法,考查弦长的求法,解题时要认真审题,注意椭圆性质的合理运用.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
命题p∨q真,p∧q假,则四个命题p,q,¬p∨¬q,¬p∧¬q中,真命题的个数为( )
| A、0 | B、1 | C、2 | D、3 |
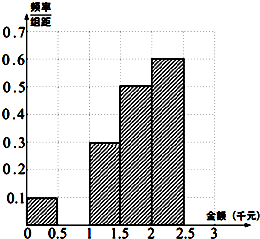 某青少年研究中心为了统计某市青少年(18岁以下)2014年春节所收压岁钱的情况进而研究青少年的消费去向,随机抽查了该市60名青少年所收压岁钱的情况,得到如下数据统计表:
某青少年研究中心为了统计某市青少年(18岁以下)2014年春节所收压岁钱的情况进而研究青少年的消费去向,随机抽查了该市60名青少年所收压岁钱的情况,得到如下数据统计表: 如图,圆内接四边形ABCD的对角线BD上有一点E,满足∠BAE=∠CAD.
如图,圆内接四边形ABCD的对角线BD上有一点E,满足∠BAE=∠CAD. 如图:在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,点M、N分别为BC、PA的中点,且PA=AB=2.
如图:在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,点M、N分别为BC、PA的中点,且PA=AB=2.