题目内容
已知函数f(x)=ax2+xlnx(a∈R)的图象在点(1,f(1))处的切线与直线x+3y=0垂直.
(Ⅰ)求实数a的值;
(Ⅱ)求证:当n>m>0时,lnn-lnm>
-
;
(Ⅲ)若存在k∈Z,使得f(x)>k恒成立,求实数k的最大值.
(Ⅰ)求实数a的值;
(Ⅱ)求证:当n>m>0时,lnn-lnm>
| m |
| n |
| n |
| m |
(Ⅲ)若存在k∈Z,使得f(x)>k恒成立,求实数k的最大值.
考点:利用导数研究函数的极值,利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)由图象在点(1,f(1))处的切线与直线x+3y=0垂直.即函数f(x)的导函数在x=1处的函数值为3,求出a的值;
(Ⅱ)利用已知函数的单调性,变形构造恒等式,从而证明不等式;
(Ⅲ)利用已知函数的单调性,构造g(x)=2x+lnx+1,由g(x)的单调性得出f(x)的单调性,再由f(x)≥f(x)极小值,解决恒等式,从而求出k的最大值.
(Ⅱ)利用已知函数的单调性,变形构造恒等式,从而证明不等式;
(Ⅲ)利用已知函数的单调性,构造g(x)=2x+lnx+1,由g(x)的单调性得出f(x)的单调性,再由f(x)≥f(x)极小值,解决恒等式,从而求出k的最大值.
解答:
解:(Ⅰ)∵f(x)=ax2+xlnx,∴f′(x)=2ax+lnx+1,
∵切线与直线x+3y=0垂直,∴切线的斜率为3,
∴f′(1)=3,即2a+1=3,故a=1;
(Ⅱ)由(Ⅰ)知f(x)=x2+xlnx,a∈(0,+∞),f′(x)=2x+lnx+1,x∈(0,+∞),
∵f′(x)在(0,+∞)上单调递增,∴当x>1时,有f′(x)>f′(1)=3>0,
∴函数f(x)在区间(1,+∞)上单调递增,
∵n>m>0,∴
>1,∴f(
)>f(1)=1
即(
)2+
ln
>1,
ln
>1-(
)2
∴lnn-lnm>
-
;
(Ⅲ)由(Ⅰ)知f(x)=x2+xlnx,a∈(0,+∞),f′(x)=2x+lnx+1,x∈(0,+∞),
令g(x)=2x+lnx+1,x∈(0,+∞),则g′(x)=2+
,x∈(0,+∞),
由g′(x)>0对x∈(0,+∞),恒成立,故g(x)在(0,+∞)上单调递增,
又∵g(
)=
-2+1=
-1<0,而g(
)=2-ln2>0,
∴存在x0∈(0,
),使g(x0)=0
∵g(x)在(0,+∞)上单调递增,
∴当x∈(0,x0)时,g(x)=f′(x)<0,f(x)在(0,x0)上单调递减;
当x∈(x0,+∞)时,g(x)=f′(x)>0,f(x)在(x0,+∞)上单调递增;
∴f(x)在x=x0处取得最小值f(x0)
∵f(x)>k恒成立,所以k<f(x0)
由g(x0)=0得,2x0+lnx0+1=0,所以lnx0=-1-2x0,
∴f(x0)=x02+x0lnx0=x02+x0(-1-2x0)=-x02-x0=-(x0+
)2+
,
又x0∈(0,
),∴f(x0)∈(-
,0),
∵k∈Z,∴k的最大值为-1.
∵切线与直线x+3y=0垂直,∴切线的斜率为3,
∴f′(1)=3,即2a+1=3,故a=1;
(Ⅱ)由(Ⅰ)知f(x)=x2+xlnx,a∈(0,+∞),f′(x)=2x+lnx+1,x∈(0,+∞),
∵f′(x)在(0,+∞)上单调递增,∴当x>1时,有f′(x)>f′(1)=3>0,
∴函数f(x)在区间(1,+∞)上单调递增,
∵n>m>0,∴
| n |
| m |
| n |
| m |
即(
| n |
| m |
| n |
| m |
| n |
| m |
| n |
| m |
| n |
| m |
| n |
| m |
∴lnn-lnm>
| m |
| n |
| n |
| m |
(Ⅲ)由(Ⅰ)知f(x)=x2+xlnx,a∈(0,+∞),f′(x)=2x+lnx+1,x∈(0,+∞),
令g(x)=2x+lnx+1,x∈(0,+∞),则g′(x)=2+
| 1 |
| x |
由g′(x)>0对x∈(0,+∞),恒成立,故g(x)在(0,+∞)上单调递增,
又∵g(
| 1 |
| e |
| 2 |
| e2 |
| 2 |
| e2 |
| 1 |
| 2 |
∴存在x0∈(0,
| 1 |
| 2 |
∵g(x)在(0,+∞)上单调递增,
∴当x∈(0,x0)时,g(x)=f′(x)<0,f(x)在(0,x0)上单调递减;
当x∈(x0,+∞)时,g(x)=f′(x)>0,f(x)在(x0,+∞)上单调递增;
∴f(x)在x=x0处取得最小值f(x0)
∵f(x)>k恒成立,所以k<f(x0)
由g(x0)=0得,2x0+lnx0+1=0,所以lnx0=-1-2x0,
∴f(x0)=x02+x0lnx0=x02+x0(-1-2x0)=-x02-x0=-(x0+
| 1 |
| 2 |
| 1 |
| 4 |
又x0∈(0,
| 1 |
| 2 |
| 3 |
| 4 |
∵k∈Z,∴k的最大值为-1.
点评:本小题主要考查函数、导数、不等式等基础知识,考查推理论证能力、运算能力,考查化归与转化思想、函数与方程思想、数形结合思想等,是一道综合性较强的导数应用题.属于难题.

练习册系列答案
相关题目
 中国的某渔船在我国的钓鱼岛海域捕鱼,渔船从A点出发(如图1所示)朝南偏西30°方向行驶同时在行驶线路上布置渔网,行驶5公里后到达预定点B转向第二预定点C,行驶7公里到达点C,再由C点行驶3公里回到起点A,求渔网围成三角形的面积以及点C在起点A的什么方向上.
中国的某渔船在我国的钓鱼岛海域捕鱼,渔船从A点出发(如图1所示)朝南偏西30°方向行驶同时在行驶线路上布置渔网,行驶5公里后到达预定点B转向第二预定点C,行驶7公里到达点C,再由C点行驶3公里回到起点A,求渔网围成三角形的面积以及点C在起点A的什么方向上.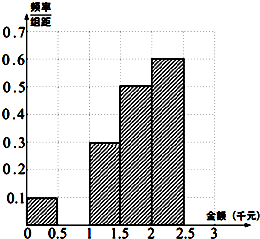 某青少年研究中心为了统计某市青少年(18岁以下)2014年春节所收压岁钱的情况进而研究青少年的消费去向,随机抽查了该市60名青少年所收压岁钱的情况,得到如下数据统计表:
某青少年研究中心为了统计某市青少年(18岁以下)2014年春节所收压岁钱的情况进而研究青少年的消费去向,随机抽查了该市60名青少年所收压岁钱的情况,得到如下数据统计表: 如图:在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,点M、N分别为BC、PA的中点,且PA=AB=2.
如图:在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,点M、N分别为BC、PA的中点,且PA=AB=2.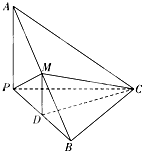 如图,已知三棱锥A-BPC中,AP⊥PC,PC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,PC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.