题目内容
已知椭圆C的方程为
+
=1(a>b>0),其离心率为
,经过椭圆焦点且垂直于长轴的弦长为3.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l:y=kx+m(|k|≤
)与椭圆C交于A、B两点,P为椭圆上的点,O为坐标原点,且满足
=
+
,求|
|的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l:y=kx+m(|k|≤
| 1 |
| 2 |
| OP |
| OA |
| OB |
| OP |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知得
,由此能求出椭圆C的方程.
(Ⅱ)由
,得(3+4k2)x2+8kmx+4m2-12=0,由此利用根的判别式、韦达定理、两点间距离公式能求出|
|的取值范围.
|
(Ⅱ)由
|
| OP |
解答:
解:(Ⅰ)由已知得
,解得a2=4,b2=3.
故椭圆C的方程为
+
=1.…(5分)
(Ⅱ)由
,消y化简整理得:
(3+4k2)x2+8kmx+4m2-12=0,
△=64k2m2-4(3+4k2)(4m2-12)=48(3+4k2-m2)>0,①
设A,B,P点的坐标分别为(x1,y1),(x2,y2),(x0,y0),
则x0=x1+x2=-
,y0=y1+y2=k(x1+x2)+2m=
.…(8分)
由于点P在椭圆C上,所以
+
=1.
从而
+
=1,化简得4m2=3+4k2,经检验满足①式.
又|OP|=
=
=
=
=
,
因为|k|≤
,得3≤4k2+3≤4,有
≤
≤1,
故
≤|OP|≤
.…(12分)
|
故椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)由
|
(3+4k2)x2+8kmx+4m2-12=0,
△=64k2m2-4(3+4k2)(4m2-12)=48(3+4k2-m2)>0,①
设A,B,P点的坐标分别为(x1,y1),(x2,y2),(x0,y0),
则x0=x1+x2=-
| 8km |
| 3+4k2 |
| 6m |
| 3+4k2 |
由于点P在椭圆C上,所以
| x02 |
| 4 |
| y02 |
| 3 |
从而
| 16k2m2 |
| (3+4k2)x2 |
| 12m2 |
| (3+4k2)2 |
又|OP|=
| x02+y02 |
|
=
|
|
4-
|
因为|k|≤
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4k2+3 |
故
| 3 |
| ||
| 2 |
点评:本题考查椭圆方程的求法,考查线段的取值范围的求法,解题时要认真审题,注意根的判别式、韦达定理、两点间距离公式的合理运用.

练习册系列答案
相关题目
下列结论不正确的是( )
| A、ex≥1+x,x∈R | ||
| B、lnx<x,x>0 | ||
| C、sinx<x,x∈(0,π) | ||
D、cosx>-
|
 中国的某渔船在我国的钓鱼岛海域捕鱼,渔船从A点出发(如图1所示)朝南偏西30°方向行驶同时在行驶线路上布置渔网,行驶5公里后到达预定点B转向第二预定点C,行驶7公里到达点C,再由C点行驶3公里回到起点A,求渔网围成三角形的面积以及点C在起点A的什么方向上.
中国的某渔船在我国的钓鱼岛海域捕鱼,渔船从A点出发(如图1所示)朝南偏西30°方向行驶同时在行驶线路上布置渔网,行驶5公里后到达预定点B转向第二预定点C,行驶7公里到达点C,再由C点行驶3公里回到起点A,求渔网围成三角形的面积以及点C在起点A的什么方向上.

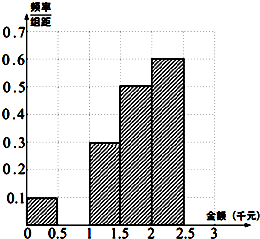 某青少年研究中心为了统计某市青少年(18岁以下)2014年春节所收压岁钱的情况进而研究青少年的消费去向,随机抽查了该市60名青少年所收压岁钱的情况,得到如下数据统计表:
某青少年研究中心为了统计某市青少年(18岁以下)2014年春节所收压岁钱的情况进而研究青少年的消费去向,随机抽查了该市60名青少年所收压岁钱的情况,得到如下数据统计表: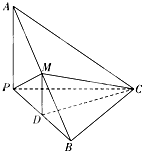 如图,已知三棱锥A-BPC中,AP⊥PC,PC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,PC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.