题目内容
已知向量
=（2cosx，
sinx），
=（cosx，2cosx），f（x）=
•
+1．
（Ⅰ）求函数f（x）的单调递增区间；
（Ⅱ）当x∈[0，
]时，求函数y=f（x）的值域．
| a |
| 3 |
| b |
| a |
| b |
（Ⅰ）求函数f（x）的单调递增区间；
（Ⅱ）当x∈[0，
| π |
| 4 |
考点：平面向量的综合题,平面向量数量积的运算,三角函数中的恒等变换应用
专题：综合题,平面向量及应用
分析：由题意，先化简f（x）=
•
+1，得到f（x）=2sin（2x+
）+2
（Ⅰ）由复合三角函数单调区间的求法，令2kπ-
≤2x+
≤2kπ+
，解之即可得出函数的增区间；
（Ⅱ）由于x∈[0，
]，先求出
≤2x+
≤
，再求出sin（2x+
）的取值范围，即可得出函数的值域．
| a |
| b |
| π |
| 6 |
（Ⅰ）由复合三角函数单调区间的求法，令2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
（Ⅱ）由于x∈[0，
| π |
| 4 |
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
| π |
| 6 |
解答：
解：由题意，f（x）=
•
+1=2cos2x+2
sinxcosx+1=cos2x+
sin2x+2=2sin（2x+
）+2 …（2分）
（Ⅰ）由2kπ-
≤2x+
≤2kπ+
，得kπ-
≤x≤kπ+
，k∈z，
所以f（x）的单调递增区间为[kπ-
，kπ+
]，k∈z …（5分）
（Ⅱ）∵x∈[0，
]，∴
≤2x+
≤
∴
≤sin（2x+
）≤1，．…（8分）
∴3≤2sin（2x+
）+2≤4，
∴函数y=f（x）的值域[3，4]…（10分）．
| a |
| b |
| 3 |
| 3 |
| π |
| 6 |
（Ⅰ）由2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
所以f（x）的单调递增区间为[kπ-
| π |
| 3 |
| π |
| 6 |
（Ⅱ）∵x∈[0，
| π |
| 4 |
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
∴
| 1 |
| 2 |
| π |
| 6 |
∴3≤2sin（2x+
| π |
| 6 |
∴函数y=f（x）的值域[3，4]…（10分）．
点评：本题考查向量与三角的综合，是近几年高考题中常见的类型，难度不大，认真计算，即可保证正确．
练习册系列答案
阅读快车系列答案
相关题目
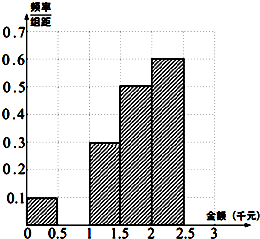某青少年研究中心为了统计某市青少年（18岁以下）2014年春节所收压岁钱的情况进而研究青少年的消费去向，随机抽查了该市60名青少年所收压岁钱的情况，得到如下数据统计表：
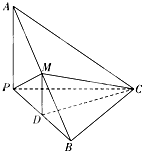如图，已知三棱锥A-BPC中，AP⊥PC，PC⊥BC，M为AB的中点，D为PB的中点，且△PMB为正三角形．