题目内容
17.已知数列{an}满足a1+a2+…+an=n2+3n(n∈N+),则$\frac{{a}_{1}^{2}}{2}+\frac{{a}_{2}^{2}}{3}+…+\frac{{a}_{n}^{2}}{n+1}$=2n2+6n.分析 通过a1+a2+…+an=n2+3n与a1+a2+…+an-1=(n-1)2+3(n-1)作差,进而计算可知an=2(n+1),分别利用等差数列、等比数列的求和公式计算即得结论.
解答 解:∵a1+a2+…+an=n2+3n,
∴当n≥2时,a1+a2+…+an-1=(n-1)2+3(n-1),
两式相减得:an=(n2+3n)-[(n-1)2+3(n-1)]=2(n+1),
又∵a1=1+3=4满足上式,
∴an=2(n+1),$\frac{{{a}_{n}}^{2}}{n+1}$=4+4n,
∴$\frac{{a}_{1}^{2}}{2}+\frac{{a}_{2}^{2}}{3}+…+\frac{{a}_{n}^{2}}{n+1}$=4n+4•$\frac{n(n+1)}{2}$=2n2+6n,
故答案为:2n2+6n.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
5.连锁水果店店主每天以每件50元购进水果若干件,以80元一件销售;若供大于求,当天剩余水果以40元一件全部退回;若供不应求,则立即从连锁店60元一件调剂,以80元一件销售.
(1)若水果店一天购进水果5件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N*)的函数解析式;
(2)店主记录了30天水果的日需求量n(单位:件)整理得表:
若水果店一天购进5件水果,以30天记录的各需求量发生的频率作为概率,求每天的利润在区间[150,200]的概率.
(1)若水果店一天购进水果5件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N*)的函数解析式;
(2)店主记录了30天水果的日需求量n(单位:件)整理得表:
| 日需求量 | 3 | 4 | 5 | 6 | 7 |
| 频数 | 2 | 3 | 15 | 6 | 4 |
12.若x,y满足约束条件$\left\{\begin{array}{l}{x+y-2≤0}\\{x-2y+1≤0}\\{2x-y+2≥0}\end{array}\right.$,则z=3x-y的最小值为( )
| A. | 3 | B. | -4 | C. | -3 | D. | -2 |
2.已知复数z满足(2+i)z=5i(其中i是虚数单位,满足i2=-1),则复数z的共轭复数是( )
| A. | -1+2i | B. | 1+2i | C. | 1-2i | D. | -1-2i |
6.设$\overrightarrow{a}$,$\overrightarrow{b}$均为非零向量,则“$\overrightarrow{a}$∥$\overrightarrow{b}$”是“$\overrightarrow{a}$与$\overrightarrow{b}$的方向相同”的( )
| A. | 充要条件 | B. | 充分但不必要条件 | ||
| C. | 必要但不充分条件 | D. | 既不充分也不必要条件 |
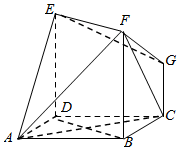 如图,矩形BDEF垂直于正方形ABCD,GC垂直于平面ABCD,且AB=DE=2CG=2.
如图,矩形BDEF垂直于正方形ABCD,GC垂直于平面ABCD,且AB=DE=2CG=2.