题目内容
12.若x,y满足约束条件$\left\{\begin{array}{l}{x+y-2≤0}\\{x-2y+1≤0}\\{2x-y+2≥0}\end{array}\right.$,则z=3x-y的最小值为( )| A. | 3 | B. | -4 | C. | -3 | D. | -2 |
分析 画出满足条件的平面区域,求出角点的坐标,结合函数的图象,从而求出z的最小值即可.
解答 解:画出满足约束条件$\left\{\begin{array}{l}{x+y-2≤0}\\{x-2y+1≤0}\\{2x-y+2≥0}\end{array}\right.$的平面区域,如图示: ,
,
由z=3x-y得到y=3x-z,
显然直线过A(-1,0)时,z最小,
z的最小值是-3,
故选:C.
点评 本题考查了简单的线性规划问题,考查数形结合思想,是一道中档题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
2.已知向量$\overrightarrow{a}$=(cosα,sinβ),$\overrightarrow{b}$=(sinα,cosβ),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则α,β的值可以是( )
| A. | α=$\frac{π}{3}$,β=-$\frac{π}{3}$ | B. | α=$\frac{π}{3}$,β=$\frac{2π}{3}$ | C. | α=$\frac{π}{5}$,β=-$\frac{7π}{10}$ | D. | α=$\frac{π}{3}$,β=-$\frac{π}{6}$ |
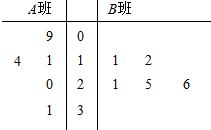 长时间用手机上网严重影响着学生的身体健康,某中学为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
长时间用手机上网严重影响着学生的身体健康,某中学为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).