题目内容

2．已知复数z满足（2+i）z=5i（其中i是虚数单位，满足i2=-1），则复数z的共轭复数是（　　）
A．-1+2iB．1+2iC．1-2iD．-1-2i

分析 根据题意，利用复数代数形式的运算法则，求出复数z与它的共轭复数$\overline{z}$即可

解答 解：复数z满足（2+i）z=5i，
∴z=$\frac{5i}{2+i}$=$\frac{5i（2-i）}{（2+i）（2-i）}$=1+2i，
故$\overline{z}$=1-2i，
故选：C．

点评 本题考查了复数代数形式的乘除运算，也考查了复数的代数表示法及其几何意义，是基础题．

练习册系列答案
相关题目
12．如图，等高的正三棱锥P-ABC与圆锥SO的底面都在平面M上，且圆O过点A，又圆O的直径AD⊥BC，垂足为E，设圆锥SO的底面半径为1，圆锥高为$\sqrt{3}$．

（1）求圆锥的侧面积；
（2）若平行于平面M的一个平面N截得三棱锥与圆锥的截面面积之比为$\frac{{\sqrt{3}}}{π}$，求三棱锥的侧棱PA与底面ABC所成角的大小．
（3）求异面直线AB与SD所成角的大小．
13．为配合上海迪斯尼游园工作，某单位设计人数的数学模型（n∈N+）：以f（n）=$\left\{\begin{array}{l}{200n+2000，n∈[1，8]}\\{360•{3}^{\frac{n-8}{12}}+3000，n∈[9，32]}\\{32400-720n，n∈[33，45]}\end{array}\right.$表示第n时进入人数，以g（n）=$\left\{\begin{array}{l}{0，n[1，18]}\\{500n-9000，n∈[19，32]}\\{8800，n∈[33，45]}\end{array}\right.$表示第n个时刻离开园区的人数；设定以15分钟为一个计算单位，上午9点15分作为第1个计算人数单位，即n=1：9点30分作为第2个计算单位，即n=2；依此类推，把一天内从上午9点到晚上8点15分分成45个计算单位：（最后结果四舍五入，精确到整数）．
（1）试计算当天14点到15点这一个小时内，进入园区的游客人数f（21）+f（22）+f（23）+f（24）、离开园区的游客人数g（21）+g（22）+g（23）+g（24）各为多少？
（2）从13点45分（即n=19）开始，有游客离开园区，请你求出这之后的园区内游客总人数最多的时刻，并说明理由：
10．已知$\overrightarrow a$=（5，4），$\overrightarrow{\;b}$=（-2，-1），$\overrightarrow c$=（x，y），若$\overrightarrow a$-2$\overrightarrow b$+3$\overrightarrow c$=$\overrightarrow 0$，则$\overrightarrow c$等于（　　）
A．（3，2）B．（-3，2）C．（3，-2）D．（-3，-2）
17．已知数列{an}满足a1+a2+…+an=n2+3n（n∈N+），则$\frac{{a}_{1}^{2}}{2}+\frac{{a}_{2}^{2}}{3}+…+\frac{{a}_{n}^{2}}{n+1}$=2n2+6n．
7．在△ABC中，角A，B，C所对应的边分别为a，b，c，若$\frac{sinA}{a}=\frac{\sqrt{3}cosC}{c}$，则∠C=60°．
14．已知数列{an}的前项和为Sn，点（n，Sn）在函数f（x）=${∫}_{1}^{x}$（2t+1）dt的图象上，则数列{an}的通项公式为（　　）
A．an=2nB．an=n2+n+2
C．an=$\left\{\begin{array}{l}{0，n=1}\\{2n-1，n≥2}\end{array}\right.$D．an=$\left\{\begin{array}{l}{0，n=1}\\{2n，n≥2}\end{array}\right.$
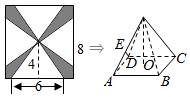11．一块边长为8cm的正方形铁片按如图所示的阴影部分裁下，然后用余下的四个全等的等腰三角加工成一个正四棱锥（底面是正方形，从顶点向底面作垂线，垂足为底面中心的四棱锥）形容器，O为底面ABCD的中心，E为棱SA的中点，则DE与SC所成角的正切值为$\frac{6\sqrt{2}}{5}$．
12．已知向量|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=2，若|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{3}$，则向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为$\frac{π}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网