题目内容
13.已知角α的顶点为坐标原点,始边为x轴正半轴,终边落在第二象限,A(x,y)是其终边上一点,向量$\overrightarrow{m}$=(3,4),若$\overrightarrow{m}$⊥$\overrightarrow{OA}$,则tan(α+$\frac{π}{4}}$)=( )| A. | 7 | B. | $-\frac{1}{7}$ | C. | -7 | D. | $\frac{1}{7}$ |
分析 根据平面向量垂直时数量积为0求出tanα,再利用两角和的正切公式求值即可.
解答 解:∵$\overrightarrow{OA}$=(x,y),向量$\overrightarrow{m}$=(3,4),且$\overrightarrow{m}$⊥$\overrightarrow{OA}$,
∴3x+4y=0,
则$\frac{y}{x}$=-$\frac{3}{4}$,
∴tanα=-$\frac{3}{4}$,
∴tan(α+$\frac{π}{4}}$)=$\frac{tanα+tan\frac{π}{4}}{1-tanαtan\frac{π}{4}}$=$\frac{-\frac{3}{4}+1}{1-(-\frac{3}{4})×1}$=$\frac{1}{7}$.
故选:D.
点评 本题考查了平面向量垂直与数量积为0的应用问题,也考查了两角和的正切公式应用问题,是基础题目.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
3.若实数x,y满足不等式组$\left\{\begin{array}{l}{2x-3y+6≥0}\\{4x-y-8≤0}\\{x+y-2≥0}\end{array}\right.$,则z=x-y的最大值为( )
| A. | -2 | B. | -1 | C. | 0 | D. | 2 |
4.若z为复数且z(2-i)=3+i,i为虚数单位,则|z|=( )
| A. | 2 | B. | $\sqrt{2}$ | C. | $\frac{74}{25}$ | D. | $\frac{\sqrt{74}}{5}$ |
1.某年级有1000名学生,随机编号为0001,0002,…,1000,现用系统抽样方法,从中抽出200人,若0122号被抽到了,则下列编号也被抽到的是( )
| A. | 0116 | B. | 0927 | C. | 0834 | D. | 0726 |
8.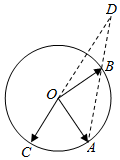 已知A,B,C为圆O上三点,CO的延长线与线段AB的延长线交于圆O外一点D,且|OD|=2|OC|,若$\overrightarrow{OC}$=p$\overrightarrow{OA}$+q$\overrightarrow{OB}$,则p+q的值为( )
已知A,B,C为圆O上三点,CO的延长线与线段AB的延长线交于圆O外一点D,且|OD|=2|OC|,若$\overrightarrow{OC}$=p$\overrightarrow{OA}$+q$\overrightarrow{OB}$,则p+q的值为( )
 已知A,B,C为圆O上三点,CO的延长线与线段AB的延长线交于圆O外一点D,且|OD|=2|OC|,若$\overrightarrow{OC}$=p$\overrightarrow{OA}$+q$\overrightarrow{OB}$,则p+q的值为( )
已知A,B,C为圆O上三点,CO的延长线与线段AB的延长线交于圆O外一点D,且|OD|=2|OC|,若$\overrightarrow{OC}$=p$\overrightarrow{OA}$+q$\overrightarrow{OB}$,则p+q的值为( )| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
3.设集合M={y|y=lgx,x>0},N={x|y=lnx,x>0},那么“a∈M”是“a∈N”的( )
| A. | 充分不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
 已知四边形PQRS是圆内接四边形,∠PSR=90°,过点Q作PR、PS的垂线,垂足分别为点H、K.
已知四边形PQRS是圆内接四边形,∠PSR=90°,过点Q作PR、PS的垂线,垂足分别为点H、K.