题目内容
在区间[-1,1]上任取两个数a、b,则点(-1,1)与点(1,1)在直线ax+by+1=0的两侧的概率等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:由题意本题满足几何概型,首先明确试验对应的去面积,然后明确满足条件的事件的区域面积,由几何概型概率公式解答.
解答:
解:由题意,本题满足几何概型,事件对应的区域的面积为2×2=4,
满足点(-1,1)与点(1,1)在直线ax+by+1=0的两侧等价于
和
,满足条件的区域面积为1,如图
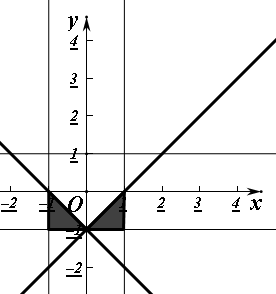
由几何概型概率公式得在区间[-1,1]上任取两个数a、b,则点(-1,1)与点(1,1)在直线ax+by+1=0的两侧的概率等于
;
故选A.
满足点(-1,1)与点(1,1)在直线ax+by+1=0的两侧等价于
|
|

由几何概型概率公式得在区间[-1,1]上任取两个数a、b,则点(-1,1)与点(1,1)在直线ax+by+1=0的两侧的概率等于
| 1 |
| 4 |
故选A.
点评:本题考查了几何概型的概率求法;关键是明确试验的区域采用的测度是长度还是面积或者体积,要由题目特征选择,本题与线性规划相结合,属于中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
复数z1=1+i,z2=3+ai,且3z1=z2,则a=( )
| A、0 | B、1 | C、2 | D、3 |
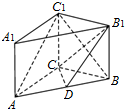 如图,已知在三棱柱ABC-A1B1C1中,AC=4,BC=3,BC1=5,点D在线段AB上,AD=3,BD=2,四边形ACC1A1为正方形.
如图,已知在三棱柱ABC-A1B1C1中,AC=4,BC=3,BC1=5,点D在线段AB上,AD=3,BD=2,四边形ACC1A1为正方形.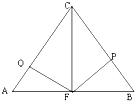 如图,CF是△ABC边AB上的高,FP⊥BC,FQ⊥AC.
如图,CF是△ABC边AB上的高,FP⊥BC,FQ⊥AC.