题目内容
13.已知直线l为曲线y=x2+x-2在点(1,0)处的切线,m为该曲线的另一条切线,且l⊥m(1)求直线m的方程
(2)求直线l、m和x轴所围成的三角形面积.
分析 (1)欲求直线m的方程,只须求出其斜率的值即可,故先利用导数求出在x=1处的导函数值,再结合l⊥m即可求出切线的斜率.从而问题解决.
(2)先通过解方程组得直线l和m的交点的坐标和l、m与x轴交点的坐标,最后根据三角形的面积公式教育处所求三角形的面积即可.
解答 解:(1)y′=2x+1,y′|x=1=3,
故切线方程是:y=3(x-1),
即直线l的方程为y=3x-3.
设直线m过曲线y=x2+x-2上的点B(b,b2+b-2),
则m的方程为y-(b2+b-2)=(2b+1)(x-b)
因为ml,则有km=2b+1=-$\frac{1}{3}$,b=-$\frac{2}{3}$.
所以直线m的方程为y=-$\frac{1}{3}$x-$\frac{22}{9}$.
(2)解方程组 $\left\{\begin{array}{l}{y=3x-3}\\{y=-\frac{1}{3}x-\frac{22}{9}}\end{array}\right.$,得 $\left\{\begin{array}{l}{x=\frac{1}{6}}\\{y=-\frac{5}{2}}\end{array}\right.$,
所以直线m和l的交点的坐标为($\frac{1}{6}$,-$\frac{5}{2}$).
l、m与x轴交点的坐标分别为(1,0)、(-$\frac{22}{3}$,0).
所以所求三角形的面积S=$\frac{1}{2}$×$\frac{25}{3}$×|-$\frac{5}{2}$|=$\frac{125}{12}$.
点评 本小题主要考查导数的几何意义,两条直线垂直的性质以及分析问题和综合运算能力.本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力.

 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案| A. | p假q假 | B. | p假q真 | C. | p真q假 | D. | p真q真 |
| A. | $\frac{f(2)}{f(0)}>2,\frac{f(0)}{{f({-2})}}>2$ | B. | f(2)>2f(0)>4f(-2) | C. | $\frac{f(2)}{f(0)}<2,\frac{f(0)}{{f({-2})}}<2$ | D. | f(2)<2f(0)<4f(-2) |
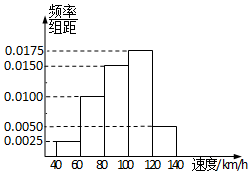 根据某固定测速点测得的某时段内过往的200辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h-120km/h,则该时段内非正常行驶的机动车辆数为30.
根据某固定测速点测得的某时段内过往的200辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h-120km/h,则该时段内非正常行驶的机动车辆数为30.