题目内容
5.若直线y=kx+2与曲线$x=\sqrt{{y^2}+6}$交于不同的两点,那么k的取值范围是( )| A. | ($-\frac{{\sqrt{15}}}{3},\frac{{\sqrt{15}}}{3}$) | B. | ($0,\frac{{\sqrt{15}}}{3}$) | C. | ($-\frac{{\sqrt{15}}}{3},0$) | D. | ($-\frac{{\sqrt{15}}}{3},-1$) |
分析 曲线$x=\sqrt{{y^2}+6}$是焦点在x轴上的双曲线的右支,由直线y=kx+2与双曲线方程联立得:(1-k2)x2-4kx-10=0,由此利用根的判别式、韦达定理,结合图象能求出k的取值范围.
解答 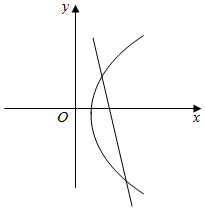 解:如图,曲线$x=\sqrt{{y^2}+6}$是焦点在x轴上的双曲线的右支,
解:如图,曲线$x=\sqrt{{y^2}+6}$是焦点在x轴上的双曲线的右支,
由直线y=kx+2与双曲线方程联立$\left\{\begin{array}{l}{y=kx+2}\\{x=\sqrt{{y}^{2}+6}}\end{array}\right.$,
消去y,得:(1-k2)x2-4kx-10=0
∵x1x2>0,∴-$\frac{10}{1-{k}^{2}}$>0,
∴k2>1,解得k>1或k<-1,
又x1+x2>0,∴$\frac{4k}{1-{k}^{2}}$>0,解得k<0,
∴k<-1,
又△=(4k2)+40(1-k2)>0,整理得k2<$\frac{5}{3}$,
解得-$\frac{\sqrt{15}}{3}$<k<$\frac{\sqrt{15}}{3}$,
∴-$\frac{\sqrt{15}}{3}<k<-1$或1<k<$\frac{\sqrt{15}}{3}$,
又由题意,直线与右支交于两点,由图象知k的取值范围是-$\frac{\sqrt{15}}{3}$<k<-1.
故选:D.
点评 本题考查实数的取值范围的求法,考查双曲线、直线方程、点到直线的距离公式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
相关题目
20.已知f(x)=$\frac{1}{x}$,则$\underset{lim}{△x→0}$$\frac{f(2+3△x)-f(2)}{△x}$的值是( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
10.某科考试题中有甲、乙两道不同类型的选做题,且每道题满分为10分,每位考生需从中任选一题作答.
(1)A同学将自己在该考试中历次的选题及得分情况统计如下:
选甲题8次,得分分别为:6,10,10,6,6,10,6,10
选乙题10次,得分分别为:5,10,9,8,9,8,10,8,5,8
某次考试中,A同学的剩余时间仅够阅读并解答出甲、乙两题中的某一道题,他应该选择甲题还是乙题?
(2)某次考试中,某班40名同学中选择甲、乙两题的人数相等,在16名该选做题获得满分的同学中有10人选的是甲题,则在犯错误概率不超过1%的情况下,判断该选做题得满分是否与选题有关?
参考公式:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
参考数据:
(1)A同学将自己在该考试中历次的选题及得分情况统计如下:
选甲题8次,得分分别为:6,10,10,6,6,10,6,10
选乙题10次,得分分别为:5,10,9,8,9,8,10,8,5,8
某次考试中,A同学的剩余时间仅够阅读并解答出甲、乙两题中的某一道题,他应该选择甲题还是乙题?
(2)某次考试中,某班40名同学中选择甲、乙两题的人数相等,在16名该选做题获得满分的同学中有10人选的是甲题,则在犯错误概率不超过1%的情况下,判断该选做题得满分是否与选题有关?
参考公式:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
参考数据:
| P(K2≥k0) | 0.1 | 0.01 | 0.001 |
| k0 | 2.706 | 6.635 | 10.828 |