题目内容
 为了解某校学生参加某项测试的情况,从该校学生中随机抽取了6位同学,这6位同学的成绩(分数)如茎叶图所示.
为了解某校学生参加某项测试的情况,从该校学生中随机抽取了6位同学,这6位同学的成绩(分数)如茎叶图所示.(1)求这6位同学成绩的平均数和标准差;
(2)从这6位同学中随机选出两位同学来分析成绩的分布情况,设ξ为这两位同学中成绩低于平均分的人数,求ξ的分布列和期望.
考点:离散型随机变量的期望与方差,茎叶图
专题:计算题,概率与统计
分析:(1)利用
=
×(76+76+78+78+82+96)与方差的计算公式计算;
(2)根据6名同学中由4人的成绩低于平均分,2人的成绩高于平均分,求出ξ分别为0,1,2的概率,列出随机变量ξ的分布列,再利用期望公式计算.
. |
| x |
| 1 |
| 6 |
(2)根据6名同学中由4人的成绩低于平均分,2人的成绩高于平均分,求出ξ分别为0,1,2的概率,列出随机变量ξ的分布列,再利用期望公式计算.
解答:
解:(1)这6位同学的成绩平均效为
=
xn=81
又s2=
(xn-
)2=
(52+52+32+32+12+152)=49
故这6位问学成绩的标准差为s=7;
(2)6名同学中由4人的成绩低于平均分,随机变量ξ可能的取值为0,1,2,
∴P(ξ=0)=
=
,P(ξ=1)=
=
,P(ξ=2)=
=
故ξ的分布列为
E(ξ)=0×
+1×
+2×
=
即ξ的数学期望
.
. |
| x |
| 1 |
| 6 |
| 6 |
 |
| n=1 |
又s2=
| 1 |
| 6 |
| 6 |
 |
| n=1 |
. |
| x |
| 1 |
| 6 |
故这6位问学成绩的标准差为s=7;
(2)6名同学中由4人的成绩低于平均分,随机变量ξ可能的取值为0,1,2,
∴P(ξ=0)=
| ||
|
| 1 |
| 15 |
| ||||
|
| 8 |
| 15 |
| ||
|
| 6 |
| 15 |
故ξ的分布列为
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 1 |
| 15 |
| 8 |
| 15 |
| 6 |
| 15 |
| 4 |
| 3 |
即ξ的数学期望
| 4 |
| 3 |
点评:本题考查了由数据的茎叶图求平均数,方差与标准差,考查了随机变量的分布列及期望,熟练掌握方差及期望的计算公式是解答本题的关键.

练习册系列答案
相关题目
已知点P(x,y)满足线性约束条件
,点M(3,1),O为坐标原点,则
•
的最大值为( )
|
| OM |
| OP |
| A、12 | B、11 | C、3 | D、-1 |
已知等差数列{an}中,a7=
,则a6+a7+a8等于( )
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
| D、111 |
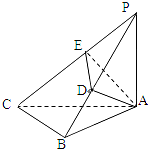 如图,已知PA⊥平面ABC,等腰直角三角形ABC中,AB=BC=2,AB⊥BC,AD⊥PB于D,AE⊥PC于E.
如图,已知PA⊥平面ABC,等腰直角三角形ABC中,AB=BC=2,AB⊥BC,AD⊥PB于D,AE⊥PC于E.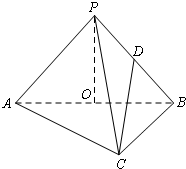 如图,三棱锥P-ABC中,已知平面PAB⊥平面ABC,AC⊥BC,AC=BC=2a,点O,D分别是AB,PB的中点,PO⊥AB,连结CD.
如图,三棱锥P-ABC中,已知平面PAB⊥平面ABC,AC⊥BC,AC=BC=2a,点O,D分别是AB,PB的中点,PO⊥AB,连结CD.