题目内容
6.设函数f(x)=1n(x+1)+a(x2-x),其中a∈R,当a=1时,求函数f(x)的极值.分析 求出原函数的导函数,确定出函数的单调区间,由此求得函数的极值点.
解答 解:函数f(x)=1n(x+1)+a(x2-x),当a=1时由f(x)=1n(x+1)+x2-x,
得f′(x)=$\frac{1}{x+1}$+2x-1=$\frac{2{x}^{2}+x}{x+1}$=$\frac{x(2x+1)}{x+1}$,x>-1.
当-1<x<$-\frac{1}{2}$,x>0时,f′(x)>0;
当$-\frac{1}{2}$<x<0时,f′(x)<0.
∴函数f(x)在(-1,$-\frac{1}{2}$),(0,+∞)上为增函数,在($-\frac{1}{2}$,0)上为减函数.
∴函数f(x)=1n(x+1)+x2-x的极大值为:f($-\frac{1}{2}$)=$\frac{3}{4}-ln2$,极小值为:f(0)=0.
点评 本题考查了利用导数研究函数的单调性,关键是正确求出原函数的导函数,是中档题.

练习册系列答案
相关题目
1.若f(x)=${∫}_{0}^{x}$|sin2t|dt(0<x<2π),则函数f(x)的单调递增区间为( )
| A. | (0,π) | B. | (0,2π) | C. | (0,t) | D. | (0,2t) |
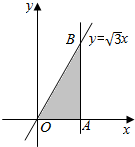 如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x,y=0,x=t(t>0)围成的△OAB的面积为S(t),则S(t)在t=2时的瞬时变化率是2$\sqrt{3}$.
如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x,y=0,x=t(t>0)围成的△OAB的面积为S(t),则S(t)在t=2时的瞬时变化率是2$\sqrt{3}$.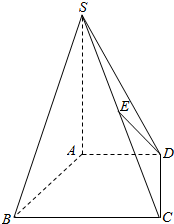 如图,在四棱锥S-ABDC中,底面ABCD是直角梯形,AB垂直于AD和BC,SA⊥底面ABCD,且SA=AB=BC=1,AD=$\frac{1}{2}$,E为SC的中点.
如图,在四棱锥S-ABDC中,底面ABCD是直角梯形,AB垂直于AD和BC,SA⊥底面ABCD,且SA=AB=BC=1,AD=$\frac{1}{2}$,E为SC的中点.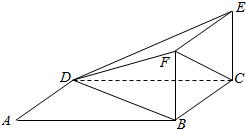 如图.ABCD为平行四边形,BCEF是边长为1的正方形.BF⊥BA,∠DAB=$\frac{π}{3}$,AB=2AD.
如图.ABCD为平行四边形,BCEF是边长为1的正方形.BF⊥BA,∠DAB=$\frac{π}{3}$,AB=2AD.