题目内容
已知函数f(x)=x2-4ax+2a+12的值域为集合M,集合N={y|y=
},M∩N=M.
(1)求实数a的取值范围;
(2)求关于x的方程
=|a-1|+2的根的取值范围.
| x |
(1)求实数a的取值范围;
(2)求关于x的方程
| x |
| a+2 |
考点:函数的值域,函数的零点与方程根的关系
专题:分类讨论,函数的性质及应用
分析:(1)先求出集合N,根据M是N的子集求出a的取值范围.
(2)在第(1)的基础上对a进行分类讨论,利用配方法求出x的取值范围.
(2)在第(1)的基础上对a进行分类讨论,利用配方法求出x的取值范围.
解答:
解:(1)∵y=
≥0,∴N∈[0,+∞),
又∵M∩N=M,∴M⊆N,即M⊆[0,+∞),
∴f(x)=x2-4ax+2a+12中的△=16a2-4(2a+12)≤0解得-
≤a≤2,
所以后a的取值范围是[-
,2].
(2)当a∈[-
,1]时,
=-(a-1)+2,x=-(a-
)2+
,∴x∈[
,
],
当a∈(1,2]时,
=(a-1)+2,x=(a+
)2-
,∴x∈(6,12],
所以x的取值范围是[
,12].
| x |
又∵M∩N=M,∴M⊆N,即M⊆[0,+∞),
∴f(x)=x2-4ax+2a+12中的△=16a2-4(2a+12)≤0解得-
| 3 |
| 2 |
所以后a的取值范围是[-
| 3 |
| 2 |
(2)当a∈[-
| 3 |
| 2 |
| x |
| a+2 |
| 1 |
| 2 |
| 25 |
| 4 |
| 9 |
| 4 |
| 25 |
| 4 |
当a∈(1,2]时,
| x |
| a+2 |
| 3 |
| 2 |
| 1 |
| 4 |
所以x的取值范围是[
| 9 |
| 4 |
点评:一、是对二次函数解析的式中参数的讨论,二、是去绝对值时要对未知参数进行讨论.分类讨论是高中数学的一个重点,也是一个难点.

练习册系列答案
相关题目
已知变量x,y满足
,则xy的最大值为( )
|
| A、1 | B、2 | C、3 | D、4 |
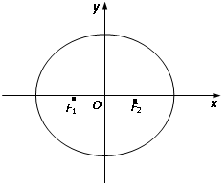 如图所示,已知椭圆C的两个焦点分别为F1(-1,0)、F2(1,0),且F2到直线x-
如图所示,已知椭圆C的两个焦点分别为F1(-1,0)、F2(1,0),且F2到直线x-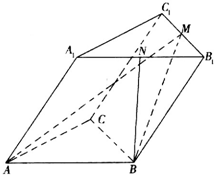 如图,已知斜三棱柱ABC-A1B1C1的底面是正三角形,点M、N分别是B1C1和A1B1的中点,AA1=AB=BM=2,∠A1AB=60°.
如图,已知斜三棱柱ABC-A1B1C1的底面是正三角形,点M、N分别是B1C1和A1B1的中点,AA1=AB=BM=2,∠A1AB=60°.