题目内容
6.设点A在-150°角的终边上,|$\overrightarrow{OA}$|=2$\sqrt{2}$(O是坐标原点),则向量$\overrightarrow{OA}$的坐标为( )| A. | ($\sqrt{6}$,$\sqrt{2}$) | B. | ($\sqrt{2}$,$\sqrt{6}$) | C. | (-$\sqrt{2}$,-$\sqrt{6}$) | D. | (-$\sqrt{6}$,-$\sqrt{2}$) |
分析 先根据点A在-150°角的终边上,|$\overrightarrow{OA}$|=2$\sqrt{2}$(O是坐标原点),点A在第三象限,根据直角三角形的边角关系求解即可、
解答 解:∵点A在-150°角的终边上,|$\overrightarrow{OA}$|=2$\sqrt{2}$(O是坐标原点),
∴点A在第三象限,且到原点的距离为$2\sqrt{2}$,
根据直角三角形的边角关系得:A的横坐标:x=-2$\sqrt{2}$cos30°=-$\sqrt{6}$.纵坐标y=-2$\sqrt{2}sin30°$=-$\sqrt{2}$
所求的坐标为(-$\sqrt{6}$,-$\sqrt{2}$).
故选:D.
点评 本题考查的知识点是平面向量的坐标运算,根据已知计算出点A的坐标得到的向量的坐标是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.如图中的程序框图表示求三个实数a,b,c中最大数的算法,那么在空白的判断框中,应该填入( )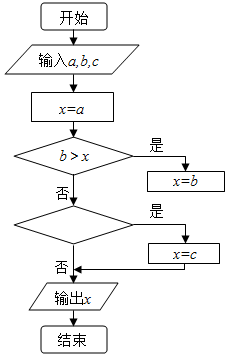

| A. | a>x | B. | b>x | C. | c<x | D. | c>x |
14.执行如图所示程序框图,则输出的结果是( )


| A. | $\frac{1}{6}$ | B. | $\frac{3}{4}$ | C. | $\frac{9}{10}$ | D. | $\frac{11}{12}$ |
1.已知双曲线C的左右焦点为F1,F2,P双曲线右支上任意一点,若以F1为圆心,以$\frac{1}{2}$|F1F2|为半径的圆与以P为圆心,|PF2|为半径的圆相切,则C的离心率为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 4 | D. | $\sqrt{3}$ |
11.已知全集U=R,A=$\left\{{x\left|{\left.{\frac{x+1}{2-x}≥0}\right\}}\right.}$,B={x|lnx<0},则A∪B=( )
| A. | {x|-1≤x≤2} | B. | {x|-1≤x<2} | C. | {x|x<-1或x≥2} | D. | {x|0<x<2} |