题目内容
19．若实数x、y满足约束条件$\left\{\begin{array}{l}{x-y+4≥0}\\{x+y≥0}\\{x≤k}\end{array}\right.$，且z=$\frac{y}{x+3}$-k的最大值为1，则z的最小值为（ ）| A． | $\frac{3}{4}$ | B． | $\frac{1}{4}$ | C． | -$\frac{1}{4}$ | D． | -$\frac{5}{4}$ |
分析 作出可行域，目标函数z=$\frac{y}{x+3}$-k表示区域内的点与（-3，0）连线的斜率减去k，结合图象和已知最大值可得k=1，解得B的坐标代值可得．
解答 解：作出约束条件$\left\{\begin{array}{l}{x-y+4≥0}\\{x+y≥0}\\{x≤k}\end{array}\right.$所对应的可行域（如图△ABC）
目标函数z=$\frac{y}{x+3}$-k表示区域内的点与P（-3，0）连线的斜率减去k，
结合图象可知当点为A（-2，2）时，z取最大值2-k=1，解得k=1，
解得此时B的坐标为（1，-1），故z的最小值为$\frac{-1}{1+3}$-1=-$\frac{5}{4}$
故选：D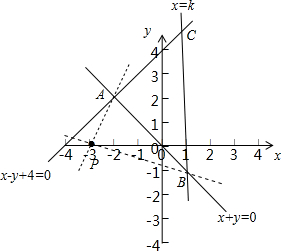
点评 本题考查简单线性规划，涉及直线的斜率公式，准确作图是解决问题的关键，属中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
10．在△ABC中，角A，B，C的对边分别为a，b，c，若（a2+b2-c2）tanC=ab，则角C的值为（ ）
| A． | $\frac{π}{6}$或$\frac{5π}{6}$ | B． | $\frac{π}{3}$或$\frac{2π}{3}$ | C． | $\frac{π}{6}$ | D． | $\frac{2π}{3}$ |
14．某高校一专业在一次自主招生中，对20名已经选拔入围的学生进行语言表达能力和逻辑思维能力测试，结果如表：
由于部分数据丢失，只知道从这20名参加测试的学生中随机抽取一人，抽到语言表达能力优秀或逻辑思维能力优秀的学生的概率为$\frac{2}{5}$．
（1）从参加测试的语言表达能力良好的学生中任意抽取2名，求其中至少有一名逻辑思维能力优秀的学生的概率；
（2）从参加测试的20名学生中任意抽取2名，设语言表达能力优秀或逻辑思维能力优秀的学生人数为X，求随机变量X的分布列及其均值．
| 语言表达能力 人数 逻辑思维能力 | 一般 | 良好 | 优秀 |
| 一般 | 2 | 2 | 1 |
| 良好 | 4 | m | 1 |
| 优秀 | 1 | 3 | n |
（1）从参加测试的语言表达能力良好的学生中任意抽取2名，求其中至少有一名逻辑思维能力优秀的学生的概率；
（2）从参加测试的20名学生中任意抽取2名，设语言表达能力优秀或逻辑思维能力优秀的学生人数为X，求随机变量X的分布列及其均值．
