题目内容
18.已知△ABC中,向量$\overrightarrow{AB}=(x,2x),\overrightarrow{AC}$=(3x,2),且∠BAC是钝角,则x的取值范围是($-\frac{4}{3},0$).分析 由∠BAC是钝角可得$\overrightarrow{AB}•\overrightarrow{AC}<0$,由已知中两个向量的坐标,代入向量数量积公式,构造不等式,分析向量反向时的情况不存在可得答案.
解答 解:∵$\overrightarrow{AB}=(x,2x),\overrightarrow{AC}$=(3x,2),且∠BAC是钝角,
∴3x2+4x<0,解得$-\frac{4}{3}<x<0$,
由$\overrightarrow{AB}=λ\overrightarrow{AC}$,得(x,2x)=λ(3x,2),
即$\left\{\begin{array}{l}{x=3λx}\\{2x=2λ}\end{array}\right.$,解得λ=0或$λ=\frac{1}{3}$,
说明两向量不存在共线反向的情况.
故x的取值范围是($-\frac{4}{3},0$).
故答案为:($-\frac{4}{3},0$).
点评 本题考查的知识点是数量积表示两个向量的夹角,其中要注意分析两向量共线反向的情况,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.若实数x、y满足约束条件$\left\{\begin{array}{l}{x-y+4≥0}\\{x+y≥0}\\{x≤k}\end{array}\right.$,且z=$\frac{y}{x+3}$-k的最大值为1,则z的最小值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{5}{4}$ |
7.阅读如图的算法框图,输出的结果S的值为( )
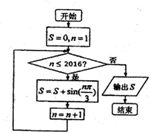

| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | 0 | D. | -$\frac{\sqrt{3}}{2}$ |