题目内容
4.双曲线的中心在原点,实轴在x轴上,与圆x2+y2=5交于点P(2,-1),如果圆在点P的切线平行于双曲线的左顶点与虚轴的一个端点的连线,求双曲线的方程.分析 设双曲线方程,将P代入双曲线方程则$\frac{4}{{a}^{2}}$-$\frac{1}{{b}^{2}}$=1,由圆的切线斜率k切与kOP的乘积为-1,k切=2,即$\frac{b}{a}$=2,则b=2a,即可求得a和b的值,求双曲线方程.
解答 解:∵双曲线的中心在原点,实轴在x轴上,
∴双曲线方程可设为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0).
∵点P(2,-1)在双曲线上,则$\frac{4}{{a}^{2}}$-$\frac{1}{{b}^{2}}$=1,①.
又∵圆x2+y2=5在点P处的切线平行于双曲线左顶点(-a,0)与虚轴的一个端点(0,b)的连线,
而圆的切线斜率k切与kOP的乘积为-1,
∴k切=2,即$\frac{b}{a}$=2,∴b=2a②.
解得①②得a2=$\frac{15}{4}$,b2=15,
∴双曲线方程为$\frac{4{x}^{2}}{15}$-$\frac{{y}^{2}}{15}$=1.
点评 本题考查双曲线的标准方程,考查直线的斜率公式,圆与双曲线的位置关系,考查计算能力,属于中档题.

练习册系列答案
相关题目
14.比较下列各组正弦值的大小
(1)sin(-$\frac{π}{10}$)>sin(-$\frac{π}{8}$)
(2)sin($\frac{7π}{8}$)<sin($\frac{5π}{8}$)
(1)sin(-$\frac{π}{10}$)>sin(-$\frac{π}{8}$)
(2)sin($\frac{7π}{8}$)<sin($\frac{5π}{8}$)
12.已知向量$\overrightarrow{a}$=(1,m),$\overrightarrow{b}$=(2,-1),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则m=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |
13.已知角θ的顶点与原点重合,始边与x轴非负半轴重合,终边过点P(-1,2),则cosθ=( )
| A. | -1 | B. | 2 | C. | $-\frac{{\sqrt{5}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
14.已知{an}为等差数列,a1+a3+a5=9,a2+a4+a6=15,则a3+a4=( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
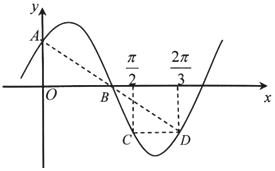 如图,已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π),点A,B分别是f(x)的图象与y轴、x轴的交点,C,D分别是f(x)的图象上横坐标为$\frac{π}{2}$、$\frac{2π}{3}$的两点,CD∥x轴,A,B,D共线.
如图,已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π),点A,B分别是f(x)的图象与y轴、x轴的交点,C,D分别是f(x)的图象上横坐标为$\frac{π}{2}$、$\frac{2π}{3}$的两点,CD∥x轴,A,B,D共线.