题目内容
若点M(2,m)(m<0)到直线l:5x-12y+n=0的距离是4,且直线l在y轴上的截距为
,则m+n= .
| 1 |
| 2 |
考点:点到直线的距离公式
专题:直线与圆
分析:由直线在y轴上的截距求得n的值,再代入点M到直线的距离求得m的值,则答案可求.
解答:
解:由点M(2,m)(m<0)到直线l:5x-12y+n=0的距离是4,
得
=4,①
由直线l:5x-12y+n=0,取x=0得,y=
.
再由直线l在y轴上的截距为
,得
=
,解得n=6.
代入①得,
=4,解得:m=
(舍),m=-3.
∴m+n=6-3=3.
故答案为:3.
得
| |2×5-12m+n| | ||
|
由直线l:5x-12y+n=0,取x=0得,y=
| n |
| 12 |
再由直线l在y轴上的截距为
| 1 |
| 2 |
| n |
| 12 |
| 1 |
| 2 |
代入①得,
| |16-12m| |
| 13 |
| 17 |
| 3 |
∴m+n=6-3=3.
故答案为:3.
点评:本题考查了点到直线的距离公式,考查了直线的截距,是基础的计算题.

练习册系列答案
相关题目
已知幂函数y=f(x)的图象过点(3,
),则f(9)=( )
| 3 |
| A、3 | ||
| B、-3 | ||
C、-
| ||
D、
|
在△ABC中,已知△ABC的面积为S=a2-(b-c)2,则有( )
| A、sinA-4cosA=4 |
| B、sinA+4cosA=4 |
| C、cosA-4sinA=4 |
| D、cosA+4sinA=4 |
在数列{an}中,a1=14,3an=3an+1+2,则使anan+2<0成立的n值是( )
| A、21 | B、22 | C、23 | D、24 |
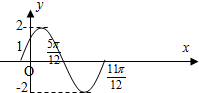 已知函数f(x)=Asin(ωx+φ)(A>0,w>0,|φ|<π)在一个周期内的图象如下图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,w>0,|φ|<π)在一个周期内的图象如下图所示.