题目内容
设函数f(x)=(x-1)ex-kx2(其中k∈R).
(1)当k=1时,求函数f(x)的单调区间和极值;
(2)当k∈[0,+∞)时,判断函数f(x)在R上的零点个数,并说明理由.
(1)当k=1时,求函数f(x)的单调区间和极值;
(2)当k∈[0,+∞)时,判断函数f(x)在R上的零点个数,并说明理由.
考点:利用导数研究函数的极值,函数零点的判定定理
专题:导数的综合应用
分析:(1)当k=1时,f(x)=(x-1)ex-x2,f′(x)=xex-2x=x(ex-2),令f′(x)=0,解得x=0或ln2.列表研究函数的单调性极值即可.
(2)f′(x)=x(ex-2k),当x<1时,f(x)<0,因此函数f(x)在(-∞,1)上无零点.
下面判定函数f(x)在[1,+∞)上零点的个数.分类讨论:k∈[0,
],k∈(
,+∞)时,通过当时研究函数的单调性极值即可得出.
(2)f′(x)=x(ex-2k),当x<1时,f(x)<0,因此函数f(x)在(-∞,1)上无零点.
下面判定函数f(x)在[1,+∞)上零点的个数.分类讨论:k∈[0,
| e |
| 2 |
| e |
| 2 |
解答:
解:(1)当k=1时,f(x)=(x-1)ex-x2,
f′(x)=xex-2x=x(ex-2),
令f′(x)=0,解得x=0或ln2.列表如下:
由表格可知:函数f(x)的单调递增区间为(-∞,0),(ln2,+∞);单调递减区间为(0,ln2).
极大值为f(0)=-1,极小值为f(ln2)=-ln22+2(ln2-1).
(2)f′(x)=x(ex-2k),当x<1时,f(x)<0,因此函数f(x)在(-∞,1)上无零点.
下面判定函数f(x)在[1,+∞)上零点的个数.
①若k∈[0,
],则当x≥1时,f′(x)≥0,函数f(x)在[1,+∞)上单调递增,且f(1)=-k≤0,f(2)=e2-4k>0,
∴函数f(x)在区间[1,2)内由一个零点,且在[1,+∞)上也只有这个零点.
②当k∈(
,+∞)时,函数f(x)在[1,ln2k)上单调递减,在(ln2k,+∞)上单调递增.
f(1)=-k<0,f(k+1)=kek+1-k(k+1)2=k(ek+1-(k+1)2),
令g(t)=et-t2,t=k+1>
+1.
g′(t)=et-2t,g″(t)=et-2,
∵t>2,∴g″(t)>0,∴g′(t)在[2,+∞)上单调递增,∴g′(t)≥g′(2)=e2-4>0,
∴g(t)在[2,+∞)上单调递增,g(t)≥g(2)=e2-4>0,
∴f(k+1)>0.
∴函数f(x)在[1,+∞)上只有一个零点.
f′(x)=xex-2x=x(ex-2),
令f′(x)=0,解得x=0或ln2.列表如下:
| x | (-∞,0) | 0 | (0,ln2) | ln2 | (ln2,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
极大值为f(0)=-1,极小值为f(ln2)=-ln22+2(ln2-1).
(2)f′(x)=x(ex-2k),当x<1时,f(x)<0,因此函数f(x)在(-∞,1)上无零点.
下面判定函数f(x)在[1,+∞)上零点的个数.
①若k∈[0,
| e |
| 2 |
∴函数f(x)在区间[1,2)内由一个零点,且在[1,+∞)上也只有这个零点.
②当k∈(
| e |
| 2 |
f(1)=-k<0,f(k+1)=kek+1-k(k+1)2=k(ek+1-(k+1)2),
令g(t)=et-t2,t=k+1>
| e |
| 2 |
g′(t)=et-2t,g″(t)=et-2,
∵t>2,∴g″(t)>0,∴g′(t)在[2,+∞)上单调递增,∴g′(t)≥g′(2)=e2-4>0,
∴g(t)在[2,+∞)上单调递增,g(t)≥g(2)=e2-4>0,
∴f(k+1)>0.
∴函数f(x)在[1,+∞)上只有一个零点.
点评:本题考查了利用导数研究函数的单调性极值、讨论函数零点的个数,考查了分类讨论的思想方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
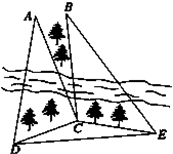 如图,某测量人员为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1百米.
如图,某测量人员为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1百米.