题目内容
已知直线l过点P（2，1），且在两个坐标轴上的截距相等，求直线l的方程．
考点：直线的截距式方程
专题：直线与圆
分析：当直线经过原点时，求得要求的方程．当直线不经过原点时，设方程为x+y=k，把点P（2，1）代入，求得k的值，可得所求的直线方程，综合可得结论．
解答：
解：当直线经过原点时，斜率为
，方程为y=
x，即x-2y=0．
当直线不经过原点时，设方程为x+y=k，把点P（2，1）代入可得2+1=k，求得k=3，故所求的直线方程为x+y=3．
综上可得，要求的直线方程为x-2y=0，或x+y=3．
| 1 |
| 2 |
| 1 |
| 2 |
当直线不经过原点时，设方程为x+y=k，把点P（2，1）代入可得2+1=k，求得k=3，故所求的直线方程为x+y=3．
综上可得，要求的直线方程为x-2y=0，或x+y=3．
点评：本题主要考查用点斜式、截距式求直线的方程，体现了分类讨论的数学思想，属于基础题．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
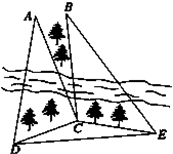如图，某测量人员为了测量西江北岸不能到达的两点A，B之间的距离，她在西江南岸找到一个点C，从C点可以观察到点A，B；找到一个点D，从D点可以观察到点A，C；找到一个点E，从E点可以观察到点B，C；并测量得到数据：∠ACD=90°，∠ADC=60°，∠ACB=15°，∠BCE=105°，∠CEB=45°，DC=CE=1百米．