题目内容
解不等式：
+
＞
．
| 1 |
| x |
| 1 |
| x+1 |
| 1 |
| x+5 |
考点：其他不等式的解法
专题：不等式的解法及应用
分析：移项、通分，把分式不等式化为
＞0（或＜0）的形式，利用同号为正、异号为负的法则，求出不等式的解集．
| f(x) |
| g(x) |
解答：
解：移项、通分，得；
＞0，
化简得，
＞0，
即
＞0；
令（x+5-2
）（x+5+2
）=0，且x（x+1）（x+5）=0，
得x=-5+2
，x=-5-2
，x=0，x=-1，x=-5；
∵-5-2
＜-5＜-1＜-5+2
＜0，
∴不等式的解集为（-5-2
，-5）∪（-1，-5+2
）∪（0，+∞）．
| (x+1)(x+5)+x(x+5)-x(x+1) |
| x(x+1)(x+5) |
化简得，
| x2+10x+5 |
| x(x+1)(x+5) |
即
(x+5-2
| ||||
| x(x+1)(x+5) |
令（x+5-2
| 5 |
| 5 |
得x=-5+2
| 5 |
| 5 |
∵-5-2
| 5 |
| 5 |
∴不等式的解集为（-5-2
| 5 |
| 5 |
点评：本题考查了分式不等式的解法与应用问题，解题时应把分式不等式化为
＞0（或＜0）的形式进行解答，是中档题题．
| f(x) |
| g(x) |
练习册系列答案
导学全程练创优训练系列答案
相关题目
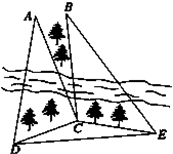如图，某测量人员为了测量西江北岸不能到达的两点A，B之间的距离，她在西江南岸找到一个点C，从C点可以观察到点A，B；找到一个点D，从D点可以观察到点A，C；找到一个点E，从E点可以观察到点B，C；并测量得到数据：∠ACD=90°，∠ADC=60°，∠ACB=15°，∠BCE=105°，∠CEB=45°，DC=CE=1百米．