题目内容
已知等差数列{an}中，a2=6，a5=15，若bn=a2n，则数列{bn}的前5项和等于 ．
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：利用等差数列的通项公式，结合已知条件列出关于a1，d的方程组，解出a1，d，可得an，进而得到bn，然后利用前n项和公式求解即可．
解答：
解：设{an}的公差为d，首项为a1，由题意得
a1+d=6，a1+4d=15
∴a1=d=3，
∴an=3n，
∴bn=a2n=6n，且b1=6，公差为6，
∴S5=5×6+
×6=90．
故答案为：90
a1+d=6，a1+4d=15
∴a1=d=3，
∴an=3n，
∴bn=a2n=6n，且b1=6，公差为6，
∴S5=5×6+
| 5×4 |
| 2 |
故答案为：90
点评：本题考查了等差数列的通项公式，以及前n项和公式，熟练应用公式是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
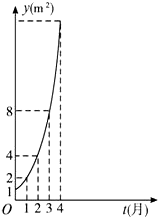如图所示是某池塘中浮萍的面积y（m2）与时间t（月）的关系y=f（t）=at，有以下叙述：
阅读如图程序框图，任意输入一次a（-1≤a≤1）与b（-1≤b≤1），则能输出数对（a，b）的概率为设集合S={x||x|＜5}，T={x|（x+7）（3-x）＞0}，则S∩T=（ ）
| A、{x|-7＜x＜-5} |
| B、{x|3＜x＜5} |
| C、{x|-5＜x＜3} |
| D、{x|-7＜x＜5} |