题目内容
20.已知函数f(x)=$lo{g}_{({a}^{2}-x)}$(2x+1)在(-$\frac{1}{2}$,0)内恒有f(x)>0,求a的取值范围.分析 由于0<2x+1<1,$lo{g}_{({a}^{2}-x)}$(2x+1)>0,所以0<a2-x<1恒成立,采用分离参数法求出a的范围.
解答 解:当x∈(-$\frac{1}{2}$,0)时,0<2x+1<1,∵$lo{g}_{({a}^{2}-x)}$(2x+1)>0恒成立,∴0<a2-x<1恒成立,
∴x<a2<1+x恒成立.∴a2≤$\frac{1}{2}$,解得-$\frac{\sqrt{2}}{2}$≤a≤$\frac{\sqrt{2}}{2}$.
∴a的取值范围是[-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$].
点评 本题考查了对数函数的图象与性质,属于基础题.

练习册系列答案
相关题目
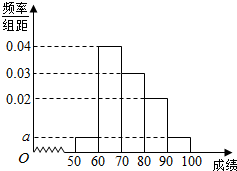 某校200位学生期末考试物理成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
某校200位学生期末考试物理成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].