题目内容
11.已知tan2θ=2tan2φ+1,则cos2θ+sin2φ的值为0.分析 利用二倍角的余弦函数公式及同角三角函数间的基本关系化简,再利用同角三角函数间的基本关系弦化切后,将已知等式代入病利用同角三角函数间的基本关系切化弦后,抵消得到结果.
解答 解:cos2θ=cos2θ-sin2θ=$\frac{co{s}^{2}θ-si{n}^{2}θ}{co{s}^{2}θ+si{n}^{2}θ}$=$\frac{1-ta{n}^{2}θ}{1+ta{n}^{2}θ}$=$\frac{-2ta{n}^{2}φ}{2ta{n}^{2}φ+2}$=$\frac{-ta{n}^{2}φ}{ta{n}^{2}φ+1}$=$\frac{-si{n}^{2}φ}{si{n}^{2}φ+co{s}^{2}φ}$=-sin2φ.
∴cos2θ+sin2φ=0.
故答案为:0.
点评 此题考查了二倍角的余弦函数公式,以及同角三角函数间的基本关系,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目
1.矩形ABCD中,AB=2$\sqrt{3}$,AD=2,点E、F分别为线段BC、CD边上的动点,且满足EF=1,则$\overrightarrow{AE}$$•\overrightarrow{AF}$的最小值是( )
| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
2.我国古代数学名著《续古摘奇算法》(杨辉)一书中有关于三阶幻方的问题:将1,2,3,4,5,6,7,8,9分别填入3×3的方格中,使得每一行,每一列及对角线上的三个数的和都相等(如图所示),我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
| 8 | 3 | 4 |
| 1 | 5 | 9 |
| 6 | 7 | 2 |
| A. | 9 | B. | 8 | C. | 6 | D. | 4 |
6.已知A(-1,0),B(2,0),平面内与点A距离为1,且与点B距离为2的直线的条数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
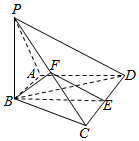 如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是棱CD和PC的中点.
如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是棱CD和PC的中点.