题目内容
8.已知△ABC中,BC长为6,周长为16,则$\overrightarrow{AB}$•$\overrightarrow{AC}$的取值范围是[7,16).分析 根据题意,画出图形,结合图形,得出$\overrightarrow{BC}$=$\overrightarrow{AC}$-$\overrightarrow{AB}$,|$\overrightarrow{AB}$|+|$\overrightarrow{AC}$|=10,两式平方相减,得出|$\overrightarrow{AB}$|×|$\overrightarrow{AB}$|+$\overrightarrow{AB}$•$\overrightarrow{AC}$=32;再利用基本不等式和向量模长的意义得出|$\overrightarrow{AB}$|×|$\overrightarrow{AC}$|的取值范围,即可求出$\overrightarrow{AB}$•$\overrightarrow{AC}$的取值范围.
解答  解:如图所示,
解:如图所示,
∵$\overrightarrow{BC}$=$\overrightarrow{AC}$-$\overrightarrow{AB}$,
∴${\overrightarrow{BC}}^{2}$=${\overrightarrow{AC}}^{2}$-2$\overrightarrow{AC}$•$\overrightarrow{AB}$+${\overrightarrow{AB}}^{2}$,
即|${\overrightarrow{AC}}^{2}$|-2|$\overrightarrow{AC}$|×|$\overrightarrow{AB}$|cosA+|${\overrightarrow{AB}}^{2}$|=36①;
又∵|$\overrightarrow{AB}$|+|$\overrightarrow{AC}$|=10,
∴|${\overrightarrow{AB}}^{2}$|+2|$\overrightarrow{AB}$|×|$\overrightarrow{AC}$|+|${\overrightarrow{AC}}^{2}$|=100②;
①-②得,2|$\overrightarrow{AB}$|×|$\overrightarrow{AC}$|(1+cosA)=64,
即|$\overrightarrow{AB}$|×|$\overrightarrow{AB}$|+$\overrightarrow{AB}$•$\overrightarrow{AC}$=32③;
由|${\overrightarrow{AB}}^{2}$|+|${\overrightarrow{AC}}^{2}$|≥2|$\overrightarrow{AB}$|×|$\overrightarrow{AC}$|,当且仅当|$\overrightarrow{AB}$|=|$\overrightarrow{AC}$|时“=”成立,
∴4|$\overrightarrow{AB}$|×|$\overrightarrow{AC}$|≤100,
∴|$\overrightarrow{AB}$|×|$\overrightarrow{AC}$|≤25,
又|$\overrightarrow{AB}$|×|$\overrightarrow{AB}$|+$\overrightarrow{AB}$•$\overrightarrow{AC}$≤|$\overrightarrow{AB}$|×|$\overrightarrow{AB}$|+|$\overrightarrow{AB}$|×|$\overrightarrow{AC}$|=2|$\overrightarrow{AB}$|×|$\overrightarrow{AB}$|,
∴|$\overrightarrow{AB}$|×|$\overrightarrow{AB}$|>16($\overrightarrow{AB}$与$\overrightarrow{AC}$不共线,不取“=”),
∴7≤$\overrightarrow{AB}$•$\overrightarrow{AC}$<16;
即$\overrightarrow{AB}$•$\overrightarrow{AC}$的取值范围是[7,16).
故答案为:[7,16).
点评 本题考查了平面向量的应用问题,也考查了三角形的边角关系的应用问题和基本不等式的应用问题,是中档题目.

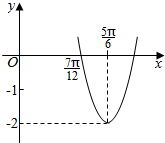
| A. | 函数f(x)在区间[0,$\frac{π}{2}$]上单调递增 | B. | 函数f(x)在区间[0,$\frac{π}{2}$]上单调递减 | ||
| C. | 函数f(x)在区间[0,$\frac{π}{2}$]上的最小值为-2 | D. | 函数f(x)在区间[0,$\frac{π}{2}$]上的最小值为-1 |
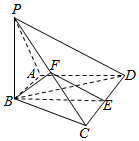 如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是棱CD和PC的中点.
如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是棱CD和PC的中点.