题目内容
一个空间几何体的三视图如图所示,则该几何体的体积为( )


A、
| ||
B、
| ||
| C、40 | ||
| D、80 |
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:几何体为其中一个侧面在下面的四棱锥,结合直观图判断棱锥的高及底面相关线段的长,把数据代入棱锥的体积公式计算.
解答:
解:由三视图知:几何体为其中一个侧面在下面的四棱锥,如图:

其中SA⊥平面ABCD,SA=4,底面ABCD为直角梯形,且AD=4,BC=1,AB=4,
∴几何体的体积V=
×
×4×4=
.
故选:A.

其中SA⊥平面ABCD,SA=4,底面ABCD为直角梯形,且AD=4,BC=1,AB=4,
∴几何体的体积V=
| 1 |
| 3 |
| 1+4 |
| 2 |
| 40 |
| 3 |
故选:A.
点评:本题考查了由三视图求几何体的体积,根据三视图判断几何体的形状及数据所对应的几何量是解答此类问题的关键.

练习册系列答案
相关题目
已知f(x)=f′(1)x2,则f′(0)等于( )
| A、0 | B、1 | C、2 | D、3 |
△ABC中,A,B为锐角,a,b,c为其三边长,如果asinA+bsinB=c,则∠C的大小为( )
| A、30° | B、45° |
| C、60° | D、90° |
| ∫ | 0 -2 |
| 4-x2 |
| A、4π | ||
| B、2π | ||
| C、π | ||
D、
|
要得到函数y=cos(2x+
)的图象,只需将y=cos2x的图象( )
| π |
| 4 |
A、向右平移
| ||
B、向左平移
| ||
C、向左平移
| ||
D、向右平移
|
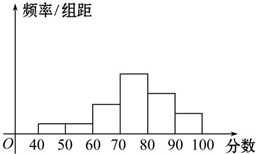 从某校参加数学竞赛的试卷中抽取一个样本,考查竞赛的成绩分布,将样本分成6组,得到频率分布直方图如图,从左到右各小组的小长方形的高的比为1:1:3:6:4:2,最右边的一组的频数是8.估计这次数学竞赛成绩的平均数
从某校参加数学竞赛的试卷中抽取一个样本,考查竞赛的成绩分布,将样本分成6组,得到频率分布直方图如图,从左到右各小组的小长方形的高的比为1:1:3:6:4:2,最右边的一组的频数是8.估计这次数学竞赛成绩的平均数