题目内容
判断直线y=2x+b能否与函数f（x）=sinx+a相切，并说明理由．
考点：函数的零点与方程根的关系
专题：计算题,导数的综合应用
分析：若直线y=2x+b能与函数f（x）=sinx+a相切，若存在导数与直线的斜率相等，求导检验即可．
解答：
解：∵f′（x）=cosx，
∴-1≤f′（x）≤1，
又∵直线y=2x+b的斜率为2；
∴直线y=2x+b不可能与函数f（x）=sinx+a相切．
∴-1≤f′（x）≤1，
又∵直线y=2x+b的斜率为2；
∴直线y=2x+b不可能与函数f（x）=sinx+a相切．
点评：本题考查了导数的几何意义，若直线y=2x+b能与函数f（x）=sinx+a相切，若存在导数与直线的斜率相等．属于基础题．
练习册系列答案
相关题目
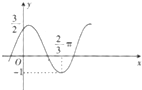将函数y=Asinωx+b（A，ω，b均为正实数）的图象向左平移| π |
| 12 |
A、y=2sin（x+
| ||||||
B、y=
| ||||||
C、y=
| ||||||
D、y=
|
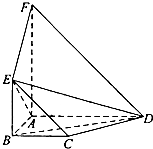如图，平面ABEF⊥平面ABCD，四边形ABEF与ABCD都是直角梯形，∠BAD=∠FAB=90°，BC
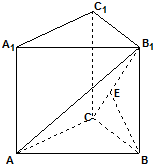如图，在直三棱柱A1B1C1-ABC中，侧面ABB1A1是边长为2的正方形，直角三角形边满足AC=BC，E是CB1上的点，且BE⊥平面ACB1．下列说法正确的是（ ）
| A、数列1，0，-1，-2与数列-2，-1，0，1是相同的数列 | ||||||||
| B、数列0，2，4，6，8，…，可记为{2n}，n∈N+ | ||||||||
C、数列{
| ||||||||
D、数列
|
如图的程序运行后，输出a的值是（ ）
| A、8 | B、7 | C、6 | D、4 |