题目内容
设非空集合S={x|m≤x≤l}满足:当x∈S时,有x2∈S.给出如下命题:
①若m=1,则S={1};
②若m=-
,则
≤l≤1;
③若l=
,则-
≤m≤0;
④若-
≤m≤0,则0≤l≤4.
其中所有正确命题的序号是 .
①若m=1,则S={1};
②若m=-
| 1 |
| 2 |
| 1 |
| 4 |
③若l=
| 1 |
| 2 |
| ||
| 2 |
④若-
| 1 |
| 2 |
其中所有正确命题的序号是
考点:元素与集合关系的判断
专题:集合
分析:根据题中条件:“当x∈S时,有x2∈S”对三个命题一一进行验证即可:对于①m=1,得
,②m=-
,则
对于③若l=
,则
,最后解出不等式,根据解出的结果与四个命题的结论对照,即可得出正确结果有几个.
|
| 1 |
| 2 |
|
| 1 |
| 2 |
|
解答:
解:由定义设非空集合S={x|m≤x≤n}满足:
当x∈S时,有x2∈S知,符合定义的参数m的值一定大于等于1或小于等于0,
惟如此才能保证m∈S时,有m2∈S即m2≥m,
符合条件的l的值一定大于等于0,小于等于1,
惟如此才能保证l∈S时,有l2∈S即l2≤l,正对各个命题进行判断:
对于①m=1,m2=1∈S故必有
,
可得l=1,S={1},
②m=-
,m2=
∈S则
,
解之可:
≤l≤1;
对于③若l=
,则
,
解之可得-
≤m≤0,
由符合条件的l的值一定大于等于0,小于等于1,可知④错误,
故正确命题的序号为:①②③.
故答案为:①②③
当x∈S时,有x2∈S知,符合定义的参数m的值一定大于等于1或小于等于0,
惟如此才能保证m∈S时,有m2∈S即m2≥m,
符合条件的l的值一定大于等于0,小于等于1,
惟如此才能保证l∈S时,有l2∈S即l2≤l,正对各个命题进行判断:
对于①m=1,m2=1∈S故必有
|
可得l=1,S={1},
②m=-
| 1 |
| 2 |
| 1 |
| 4 |
|
解之可:
| 1 |
| 4 |
对于③若l=
| 1 |
| 2 |
|
解之可得-
| ||
| 2 |
由符合条件的l的值一定大于等于0,小于等于1,可知④错误,
故正确命题的序号为:①②③.
故答案为:①②③
点评:本小题考查集合的运算及不等式和不等式组的解法.属于创新题,解答的关键是对新定义的概念的正确理解,列出不等关系转化为不等式问题解决.

练习册系列答案
相关题目
如图所示的圆锥的俯视图为( )


A、 |
B、 |
C、 |
D、 |
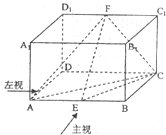 长方体ABCD-A1B1C1D1中,AA1=2,AD=3,AB=4,E,F分别在棱AB,C1D1上移动,则三棱锥F-AEC的主视图面积与左视图面积的比是( )
长方体ABCD-A1B1C1D1中,AA1=2,AD=3,AB=4,E,F分别在棱AB,C1D1上移动,则三棱锥F-AEC的主视图面积与左视图面积的比是( )