题目内容
已知全集U=R，集合A={x|2x＞1}，B={x|log2x＞2}，则A∩B=（ ）
| A、{x|x＞0} |
| B、{x|x＜-1或x＞0} |
| C、{x|x＞4} |
| D、{x|-1≤x≤4} |
考点：交集及其运算
专题：集合
分析：求出集合A，B，根据集合的交集定义进行计算．
解答：
解：依据指数函数y=2x的单调性可得集合A={x|x＞0}，依据对数函数y=log2x的定义域和单调性可得集合B={x|x＞4}，
所以A∩B={x|x＞4}．
故选：C
所以A∩B={x|x＞4}．
故选：C
点评：本题主要考查集合的基本运算，求出A，B的等价条件是解决本题的关键．
练习册系列答案
相关题目
复数z=
，则|z|=（ ）
| 1 |
| i-1 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
设全集U={x∈Z|-2＜x＜4}，A={-1，0}，B={0，1，2}，则（∁UA）∩B=（ ）
| A、{0} |
| B、{-2，-1} |
| C、{1，2} |
| D、{0，1，2} |
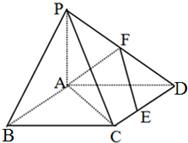如图，在四棱锥P-ABCD中，底面ABCD是正方形，PA⊥底面ABCD，且PA=PD，点F是棱PD的中点，点E为CD的中点．设a，b∈R且a+b=3，b＞0，则当
+
取得最小值时，实数a的值是（ ）
| 1 |
| 3|a| |
| |a| |
| b |
A、
| ||||
B、-
| ||||
C、-
| ||||
| D、3 |