题目内容
 如图,已知|AB|=10,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的椭圆或双曲线.若其中经过点M、N的椭圆的离心率分别是eM,eN,经过点P,Q的双曲线的离心率分别是eP,eQ,则它们的大小关系是
如图,已知|AB|=10,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的椭圆或双曲线.若其中经过点M、N的椭圆的离心率分别是eM,eN,经过点P,Q的双曲线的离心率分别是eP,eQ,则它们的大小关系是考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:首先根据椭圆和双曲线的定义得出c=5,然后数格子,得出2a=2,进而求出各自的离心率,然后进行比较.
解答:
解:由题意可知:所有的双曲线的焦距一定为|AB|=10,
即2c=10,∴c=5,
各点的对应表:(指经过该点的圆的半径)
由椭圆的第一定义得到:
对过M点的椭圆:|PA|+|PB|=2a=3+10=13,∴a=
,eM=
=
;
对过N点的椭圆:|PA|+|PB|=2a=5+7=12,∴a=6,eN=
;
由双曲线的第一定义得到:
对过P点的双曲线:||PA|-|PB||=2a=|7-3|=4,∴a=2,eP =
;
对过Q点的双曲线:||PA|-|PB||=2a=|3-8|=5,∴a=
,eQ=
=2.
∴eM<eN<eQ<eP;
故答案为:eM<eN<eQ<eP.
即2c=10,∴c=5,
各点的对应表:(指经过该点的圆的半径)
| 以A为圆心的圆的半径 | 以B为圆心的圆的半径 | |
| M | 3 | 10 |
| N | 5 | 7 |
| P | 7 | 3 |
| Q | 3 | 8 |
对过M点的椭圆:|PA|+|PB|=2a=3+10=13,∴a=
| 13 |
| 2 |
| 5 | ||
|
| 10 |
| 13 |
对过N点的椭圆:|PA|+|PB|=2a=5+7=12,∴a=6,eN=
| 5 |
| 6 |
由双曲线的第一定义得到:
对过P点的双曲线:||PA|-|PB||=2a=|7-3|=4,∴a=2,eP =
| 5 |
| 2 |
对过Q点的双曲线:||PA|-|PB||=2a=|3-8|=5,∴a=
| 5 |
| 2 |
| 5 | ||
|
∴eM<eN<eQ<eP;
故答案为:eM<eN<eQ<eP.
点评:本题考查了椭圆和双曲线的定义以及简单性质,根据格子确定a的值,和真正懂得双曲线的定义,是解题的关键,属于基础题.

练习册系列答案
相关题目
已知f(x)=f′(1)x2,则f′(0)等于( )
| A、0 | B、1 | C、2 | D、3 |
方程
=
表示的曲线为( )
| (x-2)2+(y-2)2 |
| |3x-4y-6| |
| 5 |
| A、抛物线 | B、椭圆 | C、双曲线 | D、圆 |
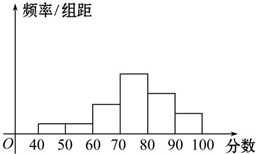 从某校参加数学竞赛的试卷中抽取一个样本,考查竞赛的成绩分布,将样本分成6组,得到频率分布直方图如图,从左到右各小组的小长方形的高的比为1:1:3:6:4:2,最右边的一组的频数是8.估计这次数学竞赛成绩的平均数
从某校参加数学竞赛的试卷中抽取一个样本,考查竞赛的成绩分布,将样本分成6组,得到频率分布直方图如图,从左到右各小组的小长方形的高的比为1:1:3:6:4:2,最右边的一组的频数是8.估计这次数学竞赛成绩的平均数