题目内容
已知函数f(x)=(x-a)(x-b)2,(0<a<b),g(x)=k(x-b),(k∈R).
(1)讨论函数f(x)在R上的单调性;
(2)讨论f(x)与g(x)的交点个数.
(1)讨论函数f(x)在R上的单调性;
(2)讨论f(x)与g(x)的交点个数.
考点:利用导数研究函数的单调性,函数的图象
专题:综合题,导数的概念及应用
分析:(1)求导数,利用导数的正负,可得函数f(x)在R上的单调性;
(2)由f(x)=g(x)得(x-a)(x-b)2=k(x-b),再分类讨论,即可讨论f(x)与g(x)的交点个数.
(2)由f(x)=g(x)得(x-a)(x-b)2=k(x-b),再分类讨论,即可讨论f(x)与g(x)的交点个数.
解答:
解:f(x)=(x-b)2+2(x-a)(x-b)=(x-b)(3x-2a-b),
∵0<a<b,∴b>
∴单调递增区间是:(-∞,
),(b,+∞),
单调递减区间是:(
,b)(6分)
(2)由f(x)=g(x)得(x-a)(x-b)2=k(x-b),(x-b)[x2-(a+b)x+ab-k]=0
讨论x2-(a+b)x+ab-k=0根的个数,
当x=b是x2-(a+b)x+ab-k=0的根时,代入得:b2-b(a+b)+ab-k=0,∴k=0
∴当k=0时,方程两根为x1=a,x2=b
∴当k=0时f(x)与g(x)有2个交点,…(8分)
当x=b不是x2-(a+b)x+ab-k=0(*)的根时,则k≠0△=(a+b)2-4(ab-k)=(a-b)2+4k
∴k<-
,方程(*)无解,k=-
,方程(*)有一个解,k>-
,且k≠0,方程(*)有2个解,且根不为x≠b.
∴综上所述,当k<-
,f(x)与g(x)有1个交点
当k=0或-
,f(x)与g(x)有2个交点
当k>-
,且k≠0,f(x)与g(x)有3个交点 …(14分)
∵0<a<b,∴b>
| 2a+b |
| 3 |
∴单调递增区间是:(-∞,
| 2a+b |
| 3 |
单调递减区间是:(
| 2a+b |
| 3 |
(2)由f(x)=g(x)得(x-a)(x-b)2=k(x-b),(x-b)[x2-(a+b)x+ab-k]=0
讨论x2-(a+b)x+ab-k=0根的个数,
当x=b是x2-(a+b)x+ab-k=0的根时,代入得:b2-b(a+b)+ab-k=0,∴k=0
∴当k=0时,方程两根为x1=a,x2=b
∴当k=0时f(x)与g(x)有2个交点,…(8分)
当x=b不是x2-(a+b)x+ab-k=0(*)的根时,则k≠0△=(a+b)2-4(ab-k)=(a-b)2+4k
∴k<-
| (a-b)2 |
| 4 |
| (a-b)2 |
| 4 |
| (a-b)2 |
| 4 |
∴综上所述,当k<-
| (a-b)2 |
| 4 |
当k=0或-
| (a-b)2 |
| 4 |
当k>-
| (a-b)2 |
| 4 |
点评:本题考查利用导数研究函数的单调性,考查交点个数,考查分类讨论的数学思想,正确分类是关键.

练习册系列答案
相关题目
已知{an}的前n项和Sn=n2-6n,则当n≥4时,|a1|+|a2|+…+|an|的值是( )
| A、n2-6n-18 | ||
B、
| ||
| C、n2-6n+18 | ||
D、
|
已知集合A={x∈R|x2≤4},B={x∈Z|
≤4},则A∩B=( )
| x |
| A、(0,2) |
| B、[0,2] |
| C、{0,2} |
| D、{0,1,2} |
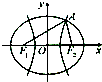 如图,F1,F2是双曲线C1:x2-
如图,F1,F2是双曲线C1:x2-