题目内容
15.已知函数的图象上相邻两个最高点的距离为π,若将函数f(x)的图象向左平移$\frac{π}{6}$个单位长度后,所得图象关于y轴对称.则f(x)的解析式为( )| A. | f(x)=2sin(x+$\frac{π}{6}$) | B. | f(x)=2sin(x+$\frac{π}{3}$) | C. | f(x)=2sin(2x+$\frac{π}{6}$) | D. | f(x)=2sin(2x+$\frac{π}{3}$) |
分析 由周期求出ω,根据y=Asin(ωx+φ)的图象变换规律、三角函数的奇偶性,求出φ的值,可得函数的解析式.
解答 解:设f(x)=2sin(ωx+φ),
∵函数的图象上相邻两个最高点的距离为π,∴$\frac{2π}{ω}$=π,ω=2.
若将函数f(x)的图象向左平移$\frac{π}{6}$个单位长度后,可得y=2sin[2(x+$\frac{π}{6}$)+φ]的图象.
根据所得图象关于y轴对称,可得$\frac{π}{3}$+φ=$\frac{π}{2}$,求得φ=$\frac{π}{6}$,
故选:C.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,根据函数的奇偶性,求出φ的值,y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
5.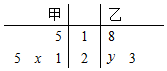 甲乙两名篮球运动员近几场比赛得分统计成茎叶图如图,甲乙两人的平均数与中位数分别相等,则x:y为( )
甲乙两名篮球运动员近几场比赛得分统计成茎叶图如图,甲乙两人的平均数与中位数分别相等,则x:y为( )
 甲乙两名篮球运动员近几场比赛得分统计成茎叶图如图,甲乙两人的平均数与中位数分别相等,则x:y为( )
甲乙两名篮球运动员近几场比赛得分统计成茎叶图如图,甲乙两人的平均数与中位数分别相等,则x:y为( )| A. | 3:2 | B. | 2:3 | C. | 3:1或5:3 | D. | 3:2或7:5 |
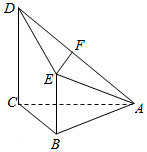 如图,四棱锥A-BCDE中,AB=BCC,BE=$\frac{1}{2}$CD.CD⊥面ABC,BE∥CD,F为AD的中点.
如图,四棱锥A-BCDE中,AB=BCC,BE=$\frac{1}{2}$CD.CD⊥面ABC,BE∥CD,F为AD的中点.