题目内容
下列函数中，在（-1，1）内有零点且单调递增的是（ ）
| A、y=log2x |
| B、y=2x-1 |
| C、y=x2-2 |
| D、y=-x3 |
考点：函数零点的判定定理,函数单调性的判断与证明
专题：函数的性质及应用
分析：根据解析式判断单调性，再根据零点存在性定理判断即可得出答案．
解答：
解：y=log
x在（-1，1）有没有意义的情况，故A不对，
y=x2-1在（-1，0）单调递减，故C不对，
y=-x3在（-1，1）单调递减，故D不对，
故A，C，D都不对，
∵y=2x-1，单调递增，f（-1）＜0，f（1）＞0，∴在（-1，1）内存在零点
故选：B
2 |
y=x2-1在（-1，0）单调递减，故C不对，
y=-x3在（-1，1）单调递减，故D不对，
故A，C，D都不对，
∵y=2x-1，单调递增，f（-1）＜0，f（1）＞0，∴在（-1，1）内存在零点
故选：B
点评：本特纳考查了函数的单调性，零点的判断，函数解析式较简单，属于容易题．
练习册系列答案
相关题目
已知x，y满足
，则x-y+1的取值范围是（ ）
|
| A、[-2，2] |
| B、[-1，2] |
| C、[-2，e] |
| D、[-1，e] |
已知命题p：a≠1或b≠2，命题q：a+b≠3，则p是q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知α∈（π，2π），cosα=-
，tan2α=（ ）
| ||
| 5 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
下列说法不正确的是（ ）
| A、“若a+b≥2，则a，b中至少有一个不小于1”的逆命题为真 |
| B、存在正实数a，b，使得lg（a+b）=1ga+1gb |
| C、命题p：?x∈R，使得x2+x-1＜0，则￢p：?x∈R，使得x2+x-1≥0 |
| D、a+b+c=0是方程ax2+bx+c=0（a≠0）有一个根为1的充分必要条件 |
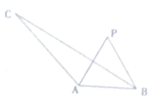如图所示，在△ABC中，∠BAC=120°，AC=3，AB=1，P为∠BAC平分线上异于A的一点，∠APB=α，三角形PAB的面积记为S．