��Ŀ����
10����֪ԲC�ķ���Ϊx2+y2=4����P��ԲC������һ���㣬����P��x��Ĵ��ߣ�����ΪH����$\overrightarrow{OQ}$=$\frac{1}{2}$��$\overrightarrow{OP}$+$\overrightarrow{OH}$��������Q�Ĺ켣ΪE���켣E��x�ᡢy���������ֱ��ڵ�A�͵�B��ֱ��y=kx��k��0����ֱ��AB�ཻ�ڵ�D����켣E�ཻ��M��N���㣮������켣E�ķ��̣�
�������ı���AMBN��������ֵ��
���� ���������⣬��Q��x��y������P��x��2y�����ٴ���Բ�ķ�����ù켣E�ķ��̣�
����$S={x_0}+\sqrt{4-{x_0}^2}$����${x_0}=2cos�ȣ�-\frac{��}{2}�ܦȡ�\frac{��}{2}��$���������ı���AMBN��������ֵ��
��� �⣺����$\overrightarrow{OQ}$=$\frac{1}{2}$��$\overrightarrow{OP}$+$\overrightarrow{OH}$��������Q��x��y������P��x��2y��
��P��x��2y����x2+y2=4�ϣ���${x^2}+{��2y��^2}=4����\frac{x^2}{4}+{y^2}=1$��
����$S={x_0}+\sqrt{4-{x_0}^2}$����${x_0}=2cos�ȣ�-\frac{��}{2}�ܦȡ�\frac{��}{2}��$��
��$S=2cos��+2sin��=2\sqrt{2}sin����+\frac{��}{4}����2\sqrt{2}$��
��${S_{max}}=2\sqrt{2}$��
���� ���⿼��켣���̵���ѵ���˴��뷨�����ߵĹ켣���̣����������ǻ�Ԫ��������ֵ�����е��⣮

��ϰ��ϵ�д�
�����Ŀ
20����֪U=R��A={x|y=ln��1-x��}��B={x|x2-x-2��0}����B�ɣ�∁UA��=��������
| A�� | {x|x��1} | B�� | {x|1��x��2} | C�� | {x|0��x��2} | D�� | {x|x��1} |
1����$��{\sqrt{3}��4}��$��ֱ��l��ax-y+1=0�ϣ���ֱ��l����б��Ϊ��������
| A�� | 30�� | B�� | 45�� | C�� | 60�� | D�� | 120�� |
5������p����1��y��x��0��a��1���� ${a^{\frac{1}{x}}}��{a^{\frac{1}{y}}}$������q����1��y��x��a��0����xa��ya���������p��q��p��q�۷�p�ܷ�q�У��������ǣ�������
| A�� | �٢� | B�� | �٢� | C�� | �ڢ� | D�� | �ڢ� |
19��������y=x2-4x+3��x��Χ�ɵķ��ͼ�ε����Ϊ��������
| A�� | $\frac{2}{3}$ | B�� | $\frac{4}{3}$ | C�� | 2 | D�� | $\frac{8}{3}$ |
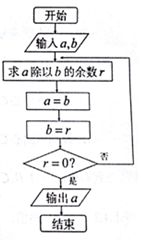 �ҹ��Ŵ������������������á�����������������������������Լ����һ��ΰ�٣����ΰ�����ҹ����ϵ��㷨-��շת�������ʵ��һ������ͼ�ij����ͼ��Դ�ڡ�շת���������������a=3051��b=1008ʱ�������a=��������
�ҹ��Ŵ������������������á�����������������������������Լ����һ��ΰ�٣����ΰ�����ҹ����ϵ��㷨-��շת�������ʵ��һ������ͼ�ij����ͼ��Դ�ڡ�շת���������������a=3051��b=1008ʱ�������a=��������