题目内容

5．命题p：若1＜y＜x，0＜a＜1，则 ${a^{\frac{1}{x}}}＜{a^{\frac{1}{y}}}$，命题q：若1＜y＜x，a＜0，则xa＜ya．在命题①p且q②p或q③非p④非q中，真命题是（　　）
A．①③B．①④C．②③D．②④

分析 分别判断出p，q的真假，从而判断出复合命题的真假即可．

解答 解：∵1＜y＜x，∴$\frac{1}{x}$＜$\frac{1}{y}$，
而0＜a＜1，则${a}^{\frac{1}{x}}$＞${a}^{\frac{1}{y}}$
故命题p是假命题；
若1＜y＜x，a＜0，则xa＜ya．
故命题q是真命题，
故①p且q是假命题，
②p或q是真命题；
③非p是真命题，
④非q是假命题，
故选：C．

点评 本题考查了复合命题的判断，考查指数函数的性质，是一道中档题．

练习册系列答案
相关题目
15．对于数列{an}，定义${H_n}=\frac{{{a_1}+2{a_2}+…+{2^{n-1}}{a_n}}}{n}$为{an}的“优值”，现在已知某数列{an}的“优值”${H_n}={2^{n+1}}$，记数列{an-kn}的前n项和为Sn，若Sn≤S5对任意的n∈N+恒成立，则实数k的最大值为$\frac{12}{5}$．
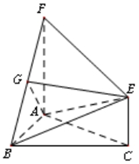16．如图，三角形ABC和梯形ACEF所在的平面互相垂直，AB⊥BC，AF⊥AC，AF∥CE且AF=2CE，G是线段BF上一点，AB=AF=BC=2．
（Ⅰ）当GB=GF时，求证：EG∥平面ABC；
（Ⅱ）求二面角E-BF-A的余弦值；
（Ⅲ）是否存在点G，满足BF⊥平面AEG？并说明理由．
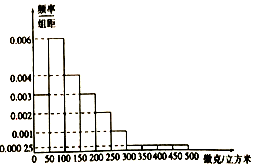13．根据环境保护部《环境空气质量指数（AQI）技术规定》，空气质量指数（AQI）在201-300之间为重度污染；在301-500之间为严重污染．依据空气质量预报，同时综合考虑空气污染程度和持续时间，将空气重污染分4个预警级别，由轻到重依次为预警四级、预警三级、预警二级、预警一级，分别用蓝、黄、橙、红颜色标示，预警一级（红色）为最高级别．（一）预警四级（蓝色）：预测未来1天出现重度污染；（二）预警三级（黄色）：预测未来1天出现严重污染或持续3天出现重度污染；（三）预警二级（橙色）；预测未来持续3天交替出现重度污染或严重污染；（四）预警一级（红色）；预测未来持续3天出现严重污染．
某城市空气质量监测部门对近300天空气中PM2.5浓度进行统计，得出这300天PM2.5浓度的频率分布直方图如图，将PM2.5浓度落入各组的频率视为概率，并假设每天的PM2.5浓度相互独立．
（1）求当地监测部门发布颜色预警的概率；
（2）据当地监测站数据显示未来4天将出现3天严重污染，求监测部门发布红色预警的概率．
20．设函数f（x）=x2-xlnx-2
（Ⅰ）求f（x）的单调区间；
（Ⅱ）若存在区间[a，b]⊆[$\frac{1}{2}$，+∞），使f（x）在[a，b]上的值域是[k（a+2），k（b+2）]，求k的取值范围．
10．已知圆C的方程为x2+y2=4，点P是圆C上任意一动点，过点P作x轴的垂线，垂足为H，且$\overrightarrow{OQ}$=$\frac{1}{2}$（$\overrightarrow{OP}$+$\overrightarrow{OH}$），动点Q的轨迹为E．轨迹E与x轴、y轴的正半轴分别交于点A和点B；直线y=kx（k＞0）与直线AB相交于点D，与轨迹E相交于M、N两点．
（Ⅰ）求轨迹E的方程；
（Ⅱ）求四边形AMBN面积的最大值．
17．在平面直角坐标系xOy中，直线l的方程为x+y-6=0，圆C的参数方程为$\left\{\begin{array}{l}x=2cosθ\\ y=2sinθ+2\end{array}\right.（{θ∈[{0，2π}）}）$，则圆心C到直线l的距离为$2\sqrt{2}$．
14．已知四棱锥P-ABCD中，$\overrightarrow{AB}=（{4，-2，3}）$，$\overrightarrow{AD}=（{-4，1，0}）$，$\overrightarrow{AP}=（{-6，2，-8}）$，则点P到底面ABCD的距离为（　　）
A．$\frac{{\sqrt{26}}}{13}$B．$\frac{{\sqrt{26}}}{26}$C．1D．2
15．已知f（x）=$\frac{{2}^{x}}{2（ln2-1）x}$，则f′（1）=1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网