题目内容
20.已知0<α<$\frac{π}{2}$<β<π,tanα=$\frac{4}{3}$,cos(β-α)=$\frac{\sqrt{2}}{10}$,则β=$\frac{3π}{4}$.分析 由条件利用同角三角函数的基本关系,求得tan(β-α) 的值,再利用两角和差的正切公式,求得tanβ=tan[(β-α)+α]的值,可得β的值.
解答 解:∵0<α<$\frac{π}{2}$<β<π,tanα=$\frac{4}{3}$,cos(β-α)=$\frac{\sqrt{2}}{10}$,∴sin(β-α)=$\sqrt{{1-cos}^{2}(β-α)}$=$\frac{7\sqrt{2}}{10}$,
∴tan(β-α)=$\frac{sin(β-α)}{cos(β-α)}$=7,∴tanβ=tan[(β-α)+α]=$\frac{tan(β-α)+tanα}{1-tan(β-α)tanα}$=$\frac{7+\frac{4}{3}}{1-7•\frac{4}{3}}$=-1,
∴β=$\frac{3π}{4}$,
故答案为:$\frac{3π}{4}$.
点评 本题主要考查同角三角函数的基本关系,两角和差的正切公式,根据三角函数的值求角,属于基础题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
11.设实数x>1,则$\frac{{x}^{2}-2x+2}{2x-2}$的最小值为( )
| A. | 2 | B. | 3 | C. | 1 | D. | $\frac{1}{2}$ |
 已知三棱柱ABC-A1B1C1,CB⊥平面BAA1B1,且四边形BAA1B1是正方形,M,N分别是AA1,BC的中点.
已知三棱柱ABC-A1B1C1,CB⊥平面BAA1B1,且四边形BAA1B1是正方形,M,N分别是AA1,BC的中点.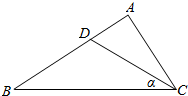 在△ABC中,BC=2AC,cosC=$\frac{3}{5}$,D是AB上的点,∠BCD=α,S△ACD:S△BCD=1:2.
在△ABC中,BC=2AC,cosC=$\frac{3}{5}$,D是AB上的点,∠BCD=α,S△ACD:S△BCD=1:2.