题目内容

9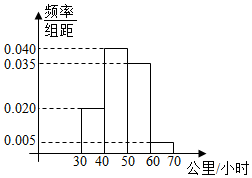．某公路的一个下穿隧道限速60公里/小时，现监控了200辆经过该隧道的车速，将这200个数据作成了频率分布直方图（如图）．
（1）请估计这200辆车的平均速度是多少？
（2）现从下穿隧道车辆中随机抽取两辆，求恰有一辆超速的概率．（以频率当概率）

分析 （1）根据平均数数的定义和组中值即可求出，
（2）先求出超速的有200×0.005×10=10辆，根据古典概率公式计算即可．

解答 解：（1）35×0.02×10+45×0.04×10+55×0.035×10+65×0.005×10=47.5公里/小时，
（2）超速的有200×0.005×10=10辆，从下穿隧道车辆中随机抽取两辆，恰有一辆超速的概率为P=$\frac{{C}_{190}^{1}{C}_{10}^{1}}{{C}_{200}^{2}}$=$\frac{19}{199}$．

点评 本题考查了频率分布直方图和古典概率的问题，属于基础题．

练习册系列答案
相关题目
7．已知两点P（4，0），Q（0，2），则以线段PQ为直径的圆的方程是（　　）
A．（x+2）2+（y+1）2=5B．（x-2）2+（y-1）2=10C．（x-2）2+（y-1）2=5D．（x+2）2+（y+1）2=10
20．圆（x-1）2+y2=1被直线$x-\sqrt{3}y=0$分成两段圆弧，则较短弧长与较长弧长之比为（　　）
A．1：2B．1：3C．1：4D．1：5
17．已知集合M={（x，y）|x=0}，N={（x，y）|y=x+2}，则M∩N=（　　）
A．{0}B．{（0，2）}C．{2}D．{（2，0）}
4．已知对任意的x∈（-∞，0）∪（0，+∞），y∈[-1，1]，不等式x2+$\frac{16}{{x}^{2}}$-2xy-$\frac{8}{x}$$\sqrt{1-{y}^{2}}$-a≥0恒成立，则实数a的取值范围为$（-∞，8-4\sqrt{2}]$．
14．函数f（x）=$\left\{\begin{array}{l}{|lo{g}_{2}x|，0＜x≤4}\\{{2}^{|x-5|}，x＞4}\end{array}\right.$若a，b，c，d各不相同，且f（a）=f（b）=f（c）=f（d），则abcd的取值范围是（　　）
A．（24，25）B．[16，25）C．（1，25）D．（0，25]
1．已知某中学联盟举行了一次“盟校质量调研考试”活动．为了解本次考试学生的某学科成绩情况，从中抽取部分学生的分数（满分为100分，得分取正整数，抽取学生的分数均在[50，100]之内）作为样本（样本容量为n）进行统计．按照[50，60]，[60，70]，[70，80]，[80，90]，[90，100]的分组作出频率分布直方图（图1），并作出样本分数的茎叶图（图2）（茎叶图中仅列出了得分在[50，60]，[90，100]的数据）．
（Ⅰ）求样本容量n和频率分布直方图中的x、y的值；
（Ⅱ）在选取的样本中，从成绩在80分以上（含80分）的学生中随机抽取2名学生参加“省级学科基础知识竞赛”，求所抽取的2名学生中恰有一人得分在[90，100]内的概率．
18．若实数x，y满足x2+2y2+xy=1，求x+2y的最大值．
19．猜想$\sqrt{\underset{\underbrace{11…1}}{2n个}-\underset{\underbrace{22…2}}{n个}}$（n∈N*）的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网