题目内容
已知圆N的标准方程为(x-5)2+(y-6)2=a2(a>0)
(1)若点M(6,9)在圆上,求a的值;
(2)已知点P(3,3)和点Q(5,3),线段PQ(不含端点)与圆N有且只有一个公共点,求a的取值范围.
(1)若点M(6,9)在圆上,求a的值;
(2)已知点P(3,3)和点Q(5,3),线段PQ(不含端点)与圆N有且只有一个公共点,求a的取值范围.
考点:直线与圆的位置关系,点与圆的位置关系
专题:直线与圆
分析:(1)由已知得(6-5)2+(9-6)2=a2=10,由此能求出a=
.
(2)由已知得点P和点Q一个在圆外,一个在圆内,由此能求出3<a<
.
| 10 |
(2)由已知得点P和点Q一个在圆外,一个在圆内,由此能求出3<a<
| 13 |
解答:
解:(1)∵圆N的标准方程为(x-5)2+(y-6)2=a2(a>0)
点M(6,9)在圆上,
∴(6-5)2+(9-6)2=a2=10,
∵a>0,∴a=
.
(2)∵点P(3,3)和点Q(5,3),线段PQ(不含端点)与圆N有且只有一个公共点,
∴点P和点Q一个在圆外,一个在圆内,
∵|PN|=
=
,
|QN|=
=3,
∵|PN|>|QN|,∴点P在圆外,点Q在圆内,
∵线段PQ不含端点,
∴3<a<
.
点M(6,9)在圆上,
∴(6-5)2+(9-6)2=a2=10,
∵a>0,∴a=
| 10 |
(2)∵点P(3,3)和点Q(5,3),线段PQ(不含端点)与圆N有且只有一个公共点,
∴点P和点Q一个在圆外,一个在圆内,
∵|PN|=
| (3-5)2+(3-6)2 |
| 13 |
|QN|=
| (5-5)2+(3-6)2 |
∵|PN|>|QN|,∴点P在圆外,点Q在圆内,
∵线段PQ不含端点,
∴3<a<
| 13 |
点评:本题考查圆的半径的求法,考查实数的取值范围的求法,是基础题,解题时要认真审题,注意圆的性质的合理运用.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
函数y=x2+2x-1的值域是( )
| A、[-1,+∞) |
| B、[-2,+∞) |
| C、[1,+∞) |
| D、[2,+∞) |
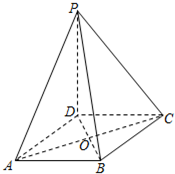 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形