题目内容
已知函数f(x)对任意实数x,y恒有f(x+y)=f(x)+f(y)且当x>0,f(x)<0,且f(1)=-2.
(1)判断f(x)的奇偶性;
(2)求f(x)在区间[-3,3]上的最大值;
(3)解关于x的不等式f(ax2)-2f(x)<f(ax)+4.
(1)判断f(x)的奇偶性;
(2)求f(x)在区间[-3,3]上的最大值;
(3)解关于x的不等式f(ax2)-2f(x)<f(ax)+4.
考点:抽象函数及其应用,函数奇偶性的判断
专题:计算题,函数的性质及应用
分析:(1)取x=y=0可得f(0)=0;再取y=-x代入即可;
(2)先判断函数的单调性,再求函数的最值;
(3)由于f(x)为奇函数,整理原式得 f(ax2)+f(-2x)<f(ax)+f(-2);即f(ax2-2x)<f(ax-2);再由函数的单调性可得ax2-2x>ax-2,从而求解.
(2)先判断函数的单调性,再求函数的最值;
(3)由于f(x)为奇函数,整理原式得 f(ax2)+f(-2x)<f(ax)+f(-2);即f(ax2-2x)<f(ax-2);再由函数的单调性可得ax2-2x>ax-2,从而求解.
解答:
解:(1)取x=y=0,
则f(0+0)=f(0)+f(0);
则f(0)=0;
取y=-x,则f(x-x)=f(x)+f(-x),
∴f(-x)=-f(x)对任意x∈R恒成立
∴f(x)为奇函数;
(2)任取x1,x2∈(-∞,+∞)且x1<x2,则x2-x1>0;
∴f(x2)+f(-x1)=f(x2-x1)<0;
∴f(x2)<-f(-x1),
又∵f(x)为奇函数
∴f(x1)>f(x2);
∴f(x)在(-∞,+∞)上是减函数;
∴对任意x∈[-3,3],恒有f(x)≤f(-3)
而f(3)=f(2+1)=f(2)+f(1)=3f(1)=-2×3=-6;
∴f(-3)=-f(3)=6;
∴f(x)在[-3,3]上的最大值为6;
(3)∵f(x)为奇函数,
∴整理原式得 f(ax2)+f(-2x)<f(ax)+f(-2);
即f(ax2-2x)<f(ax-2);
而f(x)在(-∞,+∞)上是减函数,
∴ax2-2x>ax-2;
∴(ax-2)(x-1)>0.
∴当a=0时,x∈(-∞,1);
当a=2时,x∈{x|x≠1且x∈R};
当a<0时,x∈{x|
<x<1};
当0<a<2时,x∈{x|x>
或x<1}
当a>2时,x∈{x|x<
或x>1}.
则f(0+0)=f(0)+f(0);
则f(0)=0;
取y=-x,则f(x-x)=f(x)+f(-x),
∴f(-x)=-f(x)对任意x∈R恒成立
∴f(x)为奇函数;
(2)任取x1,x2∈(-∞,+∞)且x1<x2,则x2-x1>0;
∴f(x2)+f(-x1)=f(x2-x1)<0;
∴f(x2)<-f(-x1),
又∵f(x)为奇函数
∴f(x1)>f(x2);
∴f(x)在(-∞,+∞)上是减函数;
∴对任意x∈[-3,3],恒有f(x)≤f(-3)
而f(3)=f(2+1)=f(2)+f(1)=3f(1)=-2×3=-6;
∴f(-3)=-f(3)=6;
∴f(x)在[-3,3]上的最大值为6;
(3)∵f(x)为奇函数,
∴整理原式得 f(ax2)+f(-2x)<f(ax)+f(-2);
即f(ax2-2x)<f(ax-2);
而f(x)在(-∞,+∞)上是减函数,
∴ax2-2x>ax-2;
∴(ax-2)(x-1)>0.
∴当a=0时,x∈(-∞,1);
当a=2时,x∈{x|x≠1且x∈R};
当a<0时,x∈{x|
| 2 |
| a |
当0<a<2时,x∈{x|x>
| 2 |
| a |
当a>2时,x∈{x|x<
| 2 |
| a |
点评:本题考查了抽象函数的应用,同时考查了分类讨论的数学思想,属于难题.

练习册系列答案
相关题目
已知非零向量
,
满足向量
+
与向量
-
的夹角为
,那么下列结论中一定成立的是( )
| a |
| b |
| a |
| b |
| a |
| b |
| π |
| 2 |
A、
| ||||
B、|
| ||||
C、
| ||||
D、
|
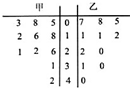 某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们在这11场比赛的得分用下面的茎叶图表示,设甲运动员得分的中位数为M1,乙运动员得分的中位数为M2,则在下列选项中,正确的是( )
某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们在这11场比赛的得分用下面的茎叶图表示,设甲运动员得分的中位数为M1,乙运动员得分的中位数为M2,则在下列选项中,正确的是( )| A、M1=18,M2=11 |
| B、M1=81,M2=12 |
| C、M1=8,M2=2 |
| D、M1=3,M2=1 |